Infinité des nombres premiers: marre d’Euclide ?

La démonstration la plus simple du fait que l’ensemble des nombres premiers est infini est sans doute la démonstration d’Euclide. C’est celle qu’on apprend aux élèves dans tous les cours de base d’arithmétique. Il s’agit d’une démonstration par l’absurde dans laquelle on suppose qu’il existe un nombre fini de nombres premiers et on construit un nombre à partir de ceux-ci qui ne peut être divisé par aucun de ces nombres premiers, d’où une contradiction:

La preuve est torchée en 7 lignes. C’est beaucoup plus que ce qu’il ne faudrait.

Cette démonstration est belle par simplicité et sa concision. Mais à force de l’avoir vue je ne sais combien de fois, on commence à en être lassé.

Pour ceux qui en ont marre d’Euclide, il existe bien d’autres preuves de l’infinité des nombres premiers (certaines plus exotiques que d’autres comme la preuve topologique de Furstenberg). Dans cet article, j’aimerais présenter, non pas une preuve de l’infinité des nombres premiers, mais quatre preuves en une ! Plus précisément, nous allons donner un modèle de preuve, qui aura le bon goût d’être accessible sans avoir beaucoup de connaissances en arithmétique. L’idée directrice de ce modèle de preuve est connue depuis longtemps et je ne prétends pas la réinventer, juste la présenter peut-être d’une manière différente.

Nombres premiers et nombres premiers entre eux

L’idée qui sera la notre est la suivante: si deux nombres sont premiers entre eux, alors les diviseurs premiers de l’un sont distincts des diviseurs premiers de l’autre. Quel est l’avantage de tout cela ? C’est simple: il est souvent difficile de déterminer explicitement les diviseurs premiers d’un nombre mais il est facile de montrer que deux nombres sont premiers entre eux (à l’aide de l’algorithme d’Euclide par exemple). Ainsi, si on réussit à montrer que deux nombres sont premiers entre eux, alors on saura qu’il existe au moins deux nombres premiers différents (si $p_1$ divise le premier nombre et $p_2$ divise le deuxième nombre, alors $p_1$ et $p_2$ sont nécessairement distincts).

Voici la proposition que nous allons utiliser pour montrer qu’il existe une infinité de nombres premiers:

S’il existe une suite $(u_n)$ d’entiers naturels >1 tels que pour tout $m>n$ , $u_m$ est premier avec $u_n$ alors l’ensemble des nombres premiers est infini.

Autrement dit, si on a une suite d’entiers qui sont deux à deux premiers entre eux, alors il existe une infinité de nombre premiers. En effet, pour tout entier naturel $n$ , il suffit de choisir un diviseur premier $p_n$ de $u_n$ (tout entier est divisible par au moins un nombre premier !). Ainsi, pour tout $m \neq n$ , $p_n$ ne peut diviser $u_m$ (car $u_m$ et $u_n$ sont premiers entre eux) et donc cela signifie que $p_n \neq p_m$ pour tout $n\neq m$ . D’où l’existence d’une infinité de nombres premiers !

Remarque: pour les psycho-rigides de l’axiome du choix, on peut choisir $p_n$ comme étant le plus petit diviseur premier de $u_n$ .

Voilà, c’est une idée simple. Il ne reste plus qu’à trouver une telle suite. Et ça, c’est plus compliqué. Heureusement, nous pouvons compter sur quatre mathématiciens qui vont nous donner quatre suites qui nous permettront d’avoir quatre démonstrations différentes. En version hollywoodienne, ça donnerait: « Quatre anciennes stars des mathématiques reviennent de leur retraite paisible pour une ultime et dernière mission. La mission de leur vie. »

Monsieur Fermat

On définit la suite $u_n$ par:

$\forall n \in \mathbb{N}, u_n = 2^{2^n}+1$

Les $u_n$ s’appellent les nombres de Fermat (les premiers termes de la suite sont donc 3, 5, 17, 257, 65537…)

Pour montrer que l’ensemble des nombres premiers est infini, il suffit de montrer que les $u_n$ sont deux à deux premiers entre eux. Eh bien, allons-y, let’s go, c’est parti les amis. Nous allons les trouver. Je sais qu’on peut y arriver.

Commençons par remarquer que les nombres de Fermat vérifient l’égalité suivante: (Une démonstration de ce résultat se trouve en fin d’article)

$\forall m>0, u_m = u_0 \times u_1 \times \hdots \times u_{m-1} + 2$

On en déduit que si $d$ est un diviseur commun à $u_m$ et $u_n$ alors $d$ divise $u_m - u_0 \times \hdots \times u_{m-1}=2$ (en effet, $u_n$ apparaît comme facteur dans le produit $u_0 \times \hdots \times u_{m-1}$ ). Ainsi, $d$ est égal à 1 ou 2. Mais si on avait $d=2$ , les nombres de Fermat $u_n$ et $u_m$ serait divisibles par 2 (puisque $d$ est un diviseur commun). Or, $2^{2^n}+1$ est un nombre impair (de la forme 2k+1) donc il ne peut pas être divisible par 2. C’est donc que $d=1$ . Ainsi, le seul diviseur commun à $u_n$ et $u_m$ est 1 et les nombres de Fermat sont donc premiers entre eux deux à deux.

Cette démonstration de l’infinité des nombres premiers est bien connue et apparaît régulièrement dans les cours d’arithmétique. Ce qui fait qu’elle marche, c’est avant tout l’égalité $u_m = u_0 \times \hdots \times u_{m-1} + 2$ .

Monsieur Sylvester

En m’inspirant de cette égalité, je me suis dit qu’une suite $(u_n)$ qui vérifierait la relation:

$\forall m>n, u_m = u_0 \times u_1 \times \hdots \times u_{m-1} + 1$

donnerait elle aussi une suite d’entiers premiers entre eux deux à deux. Cette égalité est évidemment vérifiée par la suite $(u_n)$ définie par récurrence par (qui l’eut cru ?):

$\begin{cases} u_0 &= 2 \\ u_{n+1} &= u_0 \times u_1 \times \hdots \times u_{n} + 1\\ \end{cases}$

Si $d$ est un diviseur commun à $u_m$ et $u_n$ ( $m>n$ ) alors $d$ divise $u_m - u_0 \times \hdots \times u_{m-1} = 1$ ce qui entraîne que $d=1$ et les nombres $u_m$ et $u_n$ sont donc premiers entre eux. Cela montre encore qu’il existe une infinité de nombres premiers !

Après quelques recherches, j’ai découvert que cette suite avait un nom et s’appelait la suite de Sylvester. Vous remarquez qu’on retrouve ici la preuve d’Euclide ! En effet, Euclide définissait le nombre $N = p_1 p_2 \hdots p_n + 1$ et montrait que ce nombre était premier avec tous les $p_k$ ( $1 \leq k \leq n$ ).

Les deux suites suivantes sont deux sous-suites de deux suites très célèbres, mais j’avoue que je n’ai jamais vu nulle part quelqu’un les utiliser pour montrer que l’ensemble des nombres premiers est infini.

Monsieur Mersenne

La suite des nombres de Mersenne est définie par:

$\forall n \in \mathbb{N}, u_n = 2^n-1$

Il est possible de démontrer le résultat suivant: (une démonstration de ce résultat se trouve à la fin de cet article)

$\forall m>n, PGCD(2^m-1, 2^n-1) = 2^{PGCD(m,n)}-1$

On voit donc que si on prend la restriction de cette suite à un ensemble composé d’entiers deux à deux premiers entre eux, alors les $u_n$ seront eux aussi deux à deux premiers entre eux.

Soyons plus clair en prenant un exemple. Si on choisit de prendre les termes dont les indices sont des nombres de Fermat (qui on le sait, sont deux à deux premiers entre eux) c’est-à-dire si on ne retient que les $u_n$ pour $n=3, 5, 17, 257,...$ alors la sous-suite formée sera composée d’entiers deux à deux premiers entre eux.

Pour information, voici les premiers termes de cette suite:

$\begin{array}{c|c|c} n & \text{Suite de Fermat} & \text{Sous-suite de Mersenne}\\ 0 & F_0=3 & 2^3 - 1 = 7 \\ 1 & F_1=5 & 2^5 - 1 = 31 \\ 2 & F_2 = 17 & 2^{17}-1 = 131071\\ \end{array}$

Si on formalisait cela, ça donnerait:
Soit $F_n=2^{2^n}+1$ . On définit la suite $u_n$ par:

$\forall n \in \mathbb{N}, u_n= 2^{F_n} - 1 (= 2^{2^{2^n}+1}-1)$ .

Alors, d’après la propriété citée au début de ce paragraphe, on a:

$PGCD(u_m,u_n) = 2^{PGCD(F_m,F_n)}-1$

Mais comme on a $PGCD(F_m,F_n)=1$ (les nombres de Fermat sont premiers entre eux deux à deux) alors

$PGCD(u_m,u_n)=2^1 - 1= 1$

Ainsi, cette sous-suite de la suite de Mersenne permet de montrer qu’il existe une infinité de nombres premiers ! Je sais pas vous mais de savoir que les nombres $2^{2^{2^n}+1}-1$ sont tous premiers entre eux deux à deux, ça me laisse sans voix.

Remarque: au lieu de prendre les nombres de Fermat en indice, on aurait aussi pu prendre les indices correspondant aux nombres de Sylvester à savoir les termes d’indices $n=2, 3, 7, 43...$

Monsieur Fibonacci

Last but not least, nous allons utiliser la suite de Fibonacci pour montrer qu’il existe une infinité de nombres premiers. L’idée est la même que précédemment. On va choisir une sous-suite de la suite de Fibonacci qui ne sera composée que d’entiers premiers entre eux deux à deux.

La suite de Fibonacci est définie de la façon suivante:

$\begin{cases} f_0=0 , f_1=1\\ f_{n+2}=f_{n+1}+f_n \end{cases}$

On peut démontrer la propriété suivante: (pour une démonstration, voir en fin d’article)

$\forall m>n, PGCD(f_m,f_n)=f_{PGCD(m,n)}$

Là encore, si on choisit de prendre la restriction de la suite de Fibonacci à un ensemble d’entiers deux à deux premiers entre eux, les termes de cette sous-suite seront eux aussi premiers entre eux deux à deux.

Par exemple, si on ne prend que les termes dont les indices sont des nombres de Fermat, voici les premiers termes de la sous-suite qu’on obtiendrait:

$\begin{array}{c|c|c} n & \text{Suite de Fermat} & \text{Sous-suite de Fibonacci}\\ 0 & F_0=3 & f_3 = 2 \\ 1 & F_1=5 & f_5 = 5 \\ 2 & F_2 = 17 & f_{17} = 1597\\ \end{array}$

De manière plus formelle, si on note encore $F_n$ les nombres de Fermat, et si on définit la suite $(u_n)$ par:

$\forall n, u_n = f_{F_n}= f_{2^{2^n}+1}$

alors d’après la propriété sur le PGCD, on a:

$\forall m>n, PGCD(u_m,u_n)=f_{PGCD(F_n,F_m)} = f_{1}$

Et comme on sait que $f_1=1$ , c’est que les entiers $u_m$ et $u_n$ sont premiers entre eux. Ainsi, la suite de Fibonacci nous a aussi permis de montrer qu’il existe une infinité de nombres premiers. Bon, vous allez me dire qu’utiliser une suite d’entiers premiers entre deux à deux pour construire une autre suite (complètement différente) d’entiers premiers entre eux deux à deux, ça sert à rien. Mais moi perso, ça me la coupe encore une fois.

Notes:

Voici le fichier contenant les démonstrations des propriétés intermédiaires données dans cet article, concernant les nombres de Fermat, Mersenne et Fibonacci:

Fermat, Mersenne et Fibonacci

16 commentaires pour Infinité des nombres premiers: marre d’Euclide ?

Anonyme dit :

21 octobre 2013 à 14 h 28 min

Toujours aussi sympas vos articles. Je crois que je vis pouvoir « embêter » mes TS Spé cette année avec la suite déduite des nombres de Mersenne. C’est un très beau résultat.

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  21 octobre 2013 à 17 h 51 min
  
  Merci 🙂
  Je suis content de voir que mon blog sert en pratique à mes lecteurs !
  
  J’aimeJ’aime
  
  Réponse
Anonyme dit :

23 octobre 2013 à 2 h 38 min

merci!

J’aimeJ’aime

Réponse
kikoolol dit :

16 août 2014 à 16 h 27 min

Autre méthode (j’espère que le LaTeX sera interprété) : démontrer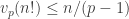 $v_{p}(n!) \leq n/(p-1)$ pour en déduire $\sqrt[n]{n!} \leq \prod_{p \mid n}{p^{1/(p-1)}}$ et conclure grâce à $(n!)^{2} \geq n^{n}$ .

J’aimeJ’aime

Réponse
- kikoolol dit :
  
  16 août 2014 à 16 h 28 min
  
  Sans LaTeX : démontrer que la p-valuation de n! est inférieure à n/(p-1) pour en déduire que la racine n-ième de n! est inférieure au produit des p^(1/(p-1)) pour p premier divisant et conclure en minorant n! par n^(n/2).
  
  J’aimeJ’aime
  
  Réponse
  - kikoolol dit :
    
    16 août 2014 à 17 h 10 min
    
    Coquille : il ne s’agit pas des nombres premiers divisant n, mais de ceux qui sont inférieurs à n, c’est-à-dire ceux qui divisent n!.
    
    J’aimeJ’aime
    
    Réponse
  - blogdemaths dit :
    
    16 août 2014 à 18 h 11 min
    
    J’ai modifié ton commentaire précédent: sur wordpress, les balises LaTeX s’ouvrent par « $latex » et se ferment avec un autre « $ »
    
    J’aimeJ’aime
    
    Réponse
kikoolol dit :

16 août 2014 à 21 h 04 min

Super, on peut mettre du $\LaTeX$ dans les commentaires ! Pour tester, je vais détailler la démonstration proposée.

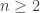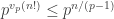Soit un entier $n \geq 2$ . Si $p$ est un nombre premier, on a $v_{p}(n!)=\lfloor n/p\rfloor+\lfloor n/p^{2}\rfloor+\dotsb \leq n/p+n/p^{2}+\dotsb=n/(p-1)$ , donc $p^{v_{p}(n!)} \leq p^{n/(p-1)}$ . En se limitant aux facteurs premiers de 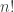$n!$ , qui sont les nombres premiers $\leq n$ , on a donc $n! \leq \prod_{p \leq n}{p^{n/(p-1)}}$ , et enfin $\sqrt[n]{n!} \leq \prod_{p \leq n}{p^{1/(p-1)}}$ .

Par ailleurs,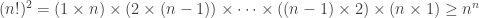
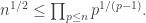$ $(n!)^{2}=(1 \times n) \times (2 \times (n-1)) \times \dotsb \times ((n-1) \times 2) \times (n \times 1) \geq n^{n}$ , soit enfin $n^{1/2} \leq \prod_{p \leq n}{p^{1/(p-1)}}.$ $

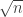S’il n’y avait qu’un nombre fini de nombres premiers, on pourrait majorer cela par le produit de tous les $p^{1/(p-1)}$ , et majorer ainsi $\sqrt{n}$ par une constante.

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  16 août 2014 à 22 h 21 min
  
  Je ne connaissais pas cette démonstration, elle est vraiment jolie !
  
  J’aimeJ’aime
  
  Réponse
  - kikoolol dit :
    
    17 août 2014 à 0 h 02 min
    
    Trop concentré à taper la démonstration, j’ai oublié la référence : « Problem solving through problems », de L. C. Larson, énoncé 5.2.14 (avec l’erreur que j’ai bêtement recopiée :-S)
    
    J’aimeJ’aime
    
    Réponse
  - kikoolol dit :
    
    17 août 2014 à 14 h 38 min
    
    S’amuser avec les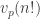 $v_{p}(n!)$ permet aussi d’obtenir des choses intéressantes sur la fonction de répartition des nombres premiers ( 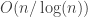$O(n/\log(n))$ sans trop d’efforts), ainsi que le postulat de Bertrand : cela pourrait vous inspirer un billet à venir 😀
    
    J’aimeJ’aime
    
    Réponse
    - blogdemaths dit :
      
      17 août 2014 à 14 h 56 min
      
      Merci pour l’idée, je garde ça dans un coin de ma tête 🙂
      
      J’aimeJ’aime
Ping : Nombres de Fermat (1ère partie): Comment Euler a factorisé F5 ? | Blogdemaths
Ping : 2 is the oddest prime: équivalent français dans le même esprit? - expressions anglais mathématiques - Apprendre la programmation, le blog
Simon dit :

30 janvier 2021 à 9 h 15 min

Bonjour
Où sont les sources ?

J’aimeJ’aime

Réponse
Anonyme dit :

31 Mai 2023 à 1 h 41 min

Bonsoir,
Voilà je suis un nouveau inscrit,
Est ce que je peux vous proposer une autre démonstration de l’infinité de l’ensemble des nombres premiers?
Cordialement.

J’aimeJ’aime

Réponse