Jusqu’où peut-on voir à l’horizon ?

C’est bientôt les grandes vacances, et vous allez peut-être profiter du soleil et de la mer durant cette période estivale. Au bord de la plage, les pieds dans l’eau, vous regarderez au loin vers l’horizon… Et là vous vous direz peut-être: mais ce point lointain à l’horizon, à quelle distance se situe-t-il ? Puis-je voir les côtes américaines si je regarde la mer depuis les plages de Bretagne ? C’est à cette question existentielle que nous allons répondre ci-dessous.

La Terre est bleue comme une orange (et ronde comme Maïté)

Comme vous le savez, la Terre est ronde (ou plutôt ellipsoïdale !), donc si vous regardez droit devant vous, il y a un moment où une partie de la Terre va être cachée. Nous allons essayer de préciser où se situe cet endroit géométriquement.

On assimile la Terre a une sphère de centre O et de rayon R=6371km. Imaginons un observateur M de hauteur h situé les pieds dans l’eau et regardant le point P à l’horizon devant lui:Puisque le rayon lumineux venant de l’horizon qui parvient aux yeux de notre observateur ne touche la Terre qu’en un seul point (l’horizon, justement !), la droite (PM) est donc une tangente à la Terre:

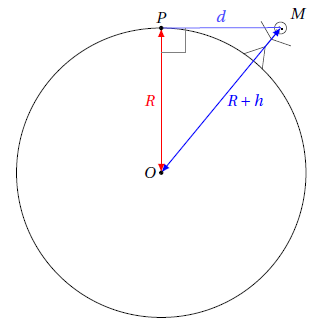Pour savoir jusqu’où on peut voir à l’horizon, il nous faut calculer la distance . Je ne vais pas faire durer le suspense plus longtemps car tout le monde voit qu’il faut utiliser le théorème de Pythagore. En effet, comme le triangle PMO est rectangle en P, on a la relation qui est équivalente à  . En développant cette dernière, on obtient :

ce qui donne

et on en déduit ainsi que:

Application numérique

Si on choisit une personne de taille moyenne, c’est-à-dire , on trouve que la distance qui la sépare de l’horizon est:

Donc, quand vous regardez à l’horizon, vous voyez seulement à environ 5km devant vous ! Je ne sais pas vous, mais j’étais persuadé qu’on voyait plus loin que cela. On n’a donc aucune chance de voir les côtes américaines depuis les côtes du Finistère… Quelle déception.

Aller plus haut…

Bon, maintenant qu’on a une formule, autant la rentabiliser. Si vous montez au sommet de la Tour Eiffel, vous verrez évidemment beaucoup plus loin à l’horizon que si vous avez les pieds au sol. Le 3ème étage étant situé à 276m au-dessus du sol, de cet endroit vous pouvez voir à 59 km à la ronde !

Depuis la tour Eiffel, vous pouvez voir jusqu’à environ 60km au loin. Sauf en cas d’alerte pollution (donc seulement 2 jours par an).
Source de l’image: http://fr.wikipedia.org/wiki/Tour_Eiffel

Et si on monte encore plus haut ? Le monument le plus grand créé par l’homme est la tour Burj Khalifa, située à Dubaï et qui mesure 828 mètres. Le 163ème et dernier étage est situé à une hauteur de 584 mètres. De cet étage, on peut donc voir à 86 km au loin !

Et à la nage ?

Remettons les pieds sur Terre et revenons au bord de la plage. Puisque la Terre est ronde, la distance à la nage et la distance à vol d’oiseau ne sont pas exactement les mêmes. Que vaut donc cette distance à la nage ?Pour faire le calcul exact de la distance à la nage, il va falloir utiliser un peu de trigonométrie élémentaire:Le fameux CAHSOHTOA™ appliqué au triangle PMO (qui est toujours rectangle, il n’a pas changé) nous donne

La distance à la nage est la longueur de l’arc de cercle bleu. On sait que la longueur de cet arc est donnée par la formule  . Ainsi,

Lorsqu’on fait l’application numérique pour un humain d’1,70m, on trouve que la distance vaut environ 4,65 km, ce qui est autant que ce qu’on avait trouvé pour la distance à vol d’oiseau (en fait les distances à vol d’oiseau et à la nage sont égales jusqu’à la 5ème décimale !).

Je ne pense pas que cela étonne grand monde que ces distances soient semblables, mais essayons tout de même de donner une explication mathématique à cela.

Équivalents

Le fait que ces distances soient très proches vient, comme on s’y attend, du fait que la taille d’un homme (ou même de la Tour Eiffel !) est très petite par rapport à celle de la Terre.

Pour le prouver, commençons par donner deux équivalents (au sens mathématique du terme). Si est voisin de 0 alors:

et

La démonstration de ces deux propriétés est donnée en fin d’article.

Si la hauteur est très petite devant le rayon alors le rapport est très proche de 0. Donc on pourra remplacer par dans les équivalents précédents:

et

Voilà donc pourquoi ces distances sont du même ordre si est petit !

Cas d’un satellite

En revanche, si on s’élève très haut dans le ciel, les distances à vol d’oiseau et à la nage vont commencer à ne plus être comparables.

Par exemple, imaginons un satellite géostationnaire, c’est-à-dire situé à une altitude h=36 000 km. La distance à vol d’oiseau est environ de 41 900 km alors que la distance au sol (« à la nage ») est environ de 9 045 de km (autrement dit, si une personne située au sol exactement sous le satellite devait marcher tout droit pour rejoindre le point le plus éloigné que le satellite peut voir, elle marcherait 9 045 km). Comme la hauteur n’est plus négligeable devant le rayon de la Terre, il n’est donc pas étonnant que ces deux valeurs ne soient plus du même ordre de grandeur.

Si on s’élève indéfiniment dans le ciel, la distance à vol d’oiseau va bien entendu tendre vers alors que la distance à la nage va tendre vers le quart de la circonférence de la Terre, comme on le devine sur l’animation ci-dessous:

En rouge, la distance à vol d’oiseau et en bleu, la distance à la nage. Si on zoome, on peut voir George Clooney dans le satellite, en train de tourner Gravity.

Voilà donc un bel exemple visuel de bijection d’un intervalle de longueur infini vers un intervalle de longueur finie !

Note:

Voici les calculs des équivalents donnés dans l’article.