Harmonique, nique, nique…

« Dominique, nique, nique,
S’en allait tout simplement,
Routier, pauvre et chantant… »

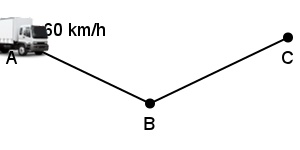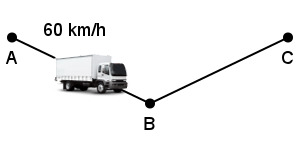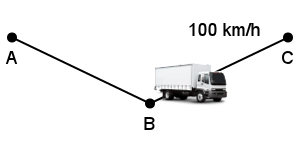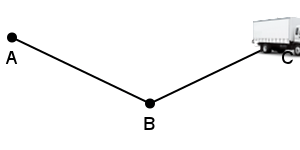
Ce matin, Dominique, routier de son métier, part d’une ville A et doit rejoindre une ville C. Pour cela, son itinéraire le fait passer par une ville B qui est à la même distance de la ville A que de la ville C.

L’histoire ne dit pas ce que transporte Dominique dans son camion… (Source: Wikipédia)

Lors de la première partie de son trajet allant de A à B, Dominique (nique, nique) roule doucement (sans doute était-il mal réveillé) et effectue le trajet de la ville A à la ville B à une vitesse de 60km/h. Arrivé à la ville B, Dominique (nique, nique) se rend compte qu’il est en retard et décide de rouler plus vite: bravant les limitations de vitesse et les forces de l’ordre, Dominique (nique, nique la police) effectue alors le trajet de la ville B à la ville C à une vitesse de 100 km/h.

Quelle était la vitesse moyenne de Dominique sur la totalité de son trajet, c’est-à-dire de la ville A à C ?

Dites camion ?

Si vous avez répondu que la vitesse moyenne de Dominique est de 80km/h, vous vous êtes malheureusement trompé car Dominique a roulé en moyenne à 75km/h. Pour l’anecdote, Dominique fut fier de dire au juge qu’il avait roulé seulement à 75km/h en moyenne, soit en dessous de la limite des 80km/h autorisés sur les routes nationales.

On the road again

Si vous ne saisissez toujours pas pourquoi il a roulé à 75km/h de moyenne pour aller de la ville A à la ville C (et il n’y a pas de honte à avoir car cela n’a rien d’intuitif), faisons les calculs pour comprendre. Attention, les calculs suivants demandent un tout petit peu de technique (nique, nique) mais pas de panique (niq… OK, on a compris).

Notons $d$ la distance séparant la ville A de la ville B, qui est aussi la distance séparant la ville B de la ville C. On note respectivement $t_1$ et $t_2$ les temps mis par Dominique pour aller de la ville A à la ville B et de la ville B à la ville C.

Je suppose que vous vous souvenez parfaitement de la formule donnant la vitesse $v$ moyenne en fonction de la distance $d$ parcourue et du temps $t$ pour la parcourir:

$v = \dfrac{d}{t}$

Puisqu’il a roulé à 60 km/h de moyenne entre la ville A et la ville B, on a donc $60 = \dfrac{d}{t_1}$ . De même, pour le trajet entre la ville B et la ville C, on a l’égalité $100 = \dfrac{d}{t_2}$ . En inversant, on a donc les relations $t_1 = \dfrac{d}{60}$ et $t_2 = \dfrac{d}{100}$ .

Maintenant, intéressons-nous à la totalité du trajet. La distance totale parcourue est $d+d = 2d$ . Le temps total mis est $t_1 + t_2$ . La vitesse moyenne $v$ pour aller de la ville A à la ville C est

$v = \dfrac{\text{distance totale}}{\text{temps total}} = \dfrac{2d}{t_1+t_2} = \dfrac{2d}{\dfrac{d}{60} + \dfrac{d}{100}} = \dfrac{2}{\dfrac{1}{60} + \dfrac{1}{100}}$

Je suppose aussi que vous savez qu’un dénominateur commun à 60 et 100 est 300 (je suppose quand même pas mal de choses sur mes lecteurs !), ce qui donne

$v = \dfrac{2}{\dfrac{5}{300} + \dfrac{3}{300}} = \dfrac{2}{\dfrac{8}{300}} = 300 \times \dfrac{2}{8} = 75$

J’espère que cela vous convainc définitivement que la vitesse moyenne de notre zélé routier n’était pas de 80km/h mais de 75km/h.Moyenne harmonique

Dans le cas général où les vitesses $v_1$ et $v_2$ des deux trajets sont quelconques, on peut démontrer de la même manière que la vitesse moyenne $v$ est donnée par la formule :

$\boxed{ v = \dfrac{2}{\dfrac{1}{v_1} + \dfrac{1}{v_2}} }$

Ce nombre s’appelle la moyenne harmonique des nombres $v_1$ et $v_2$ . En général, ce nombre est différent de la moyenne simple $\dfrac{v_1 + v_2}{2}$ qu’on appelle aussi moyenne arithmétique.

Par exemple, si au début vous avez répondu que la vitesse moyenne de Dominique est de 80km/h, c’est probablement parce que vous avez fait une moyenne arithmétique: $\dfrac{60 + 100}{2} = 80$ . Le cas de Dominique illustrait donc que, parfois, la moyenne arithmétique ne permet pas de calculer la valeur d’une moyenne et que, dans le cas d’une vitesse moyenne de deux vitesses sur des trajets de même longueur, il faut utiliser une moyenne harmonique.

Lien entre moyenne harmonique et moyenne arithmétique

Bien qu’elles ne soient en général par égales, les moyennes harmoniques et arithmétiques sont tout de même liées par une jolie relation que nous allons voir.

Avant cela, notons qu’on peut calculer la moyenne harmonique d’autant de nombres que l’on veut. Par définition, la moyenne harmonique $H(x_1, x_2, \cdots, x_n)$ de $n$ nombres $x_1, x_2, \cdots, x_n$ est

$H(x_1, x_2, \cdots, x_n) =\dfrac{n}{\dfrac{1}{x_2} + \dfrac{1}{x_2} + \cdots + \dfrac{1}{x_n}}$

Par analogie, nous noterons

$A(x_1,x_2, \cdots, x_n) = \dfrac{x_1+x_2+\cdots+x_n}{n}$

la moyenne arithmétique de ces nombres. On voit alors immédiatement que

$H(x_1, x_2, \cdots, x_n) = \dfrac{1}{A\left( \frac{1}{x_1}, \frac{1}{x_2}, \cdots, \frac{1}{x_n}\right) }$

Autrement dit, la moyenne harmonique de $n$ nombres est égale à l’inverse de la moyenne arithmétique de leurs inverses. C’est pas beau ça ?

On comprend donc un peu mieux dans quels cas utiliser la moyenne harmonique: dans des phénomènes où les grandeurs sont des quotients et qu’on souhaite déterminer un rapport moyen.

Problèmes avec des moyennes harmoniques

Maintenant qu’on sait mieux ce que représente une moyenne harmonique, j’aimerais vous présenter deux petits problèmes amusants qui la font intervenir. N’hésitez pas à essayer de les résoudre par vous-même ou bien à les proposer à votre entourage pour voir les réponses qu’on vous donne.

Le problème des peintres

Supposons qu’on ait un mur à peindre. Quatre peintres s’affairent à la tâche (d’ailleurs, un des quatre peintres est Dominique, effectuant une peine de travaux d’intérêt général, mais peu importe). Le 1er peintre pourrait peindre le mur entier tout seul en 6 heures. Le second peintre pourrait peindre tout le mur en 3 heures. Le troisième pourrait peindre tout le mur en 2 heures et le quatrième pourrait le faire en 1 heure (toujours aussi rapide ce Dominique). Si les 4 peintres peignaient ce mur en même temps, combien de temps mettraient-ils ?

Carré blanc sur fond blanc par Kasimir Malevitch (Source: Wikipédia)
Combien de temps a-t-il fallu à Kasimir Malevitch pour peindre un mur blanc en blanc ?

Tout le monde a envie de répondre $\dfrac{6+3+2+1}{4} = \dfrac{12}{4} = 3$ heures. Tout le monde. Sauf vous.

D’une part, parce que vous comprenez tout de suite que s’il y a un peintre capable de peindre le mur en 1 heure, le résultat ne peut pas être supérieur à 1. D’autre part, car vous êtes érudit à présent : vous savez ce qu’est une moyenne harmonique (et je suis fier de vous !).

Si on note $S$ la surface à peindre et $v_1 = \dfrac{S}{6}$ , $v_2 = \dfrac{S}{3}$ , $v_3 = \dfrac{S}{2}$ et $v_4 = \dfrac{S}{1}$ les vitesses de peinture des 4 peintres, alors la vitesse moyenne est:

$v = \dfrac{4}{ \dfrac{1}{v_1} + \dfrac{1}{v_2} + \dfrac{1}{v_3} + \dfrac{1}{v_4}} = \dfrac{4}{\dfrac{S}{6} + \dfrac{S}{3} + \dfrac{S}{2} + \dfrac{S}{1}} = \dfrac{4}{S \times \dfrac{12}{6}} = \dfrac{2}{S}$

Attention à l’interprétation: cela signifie que si ces 4 peintres peignaient chacun successivement 4 murs identiques, alors il faudrait en moyenne à un peintre seul une vitesse de $v = \dfrac{2}{S}$ pour peindre ces 4 murs, ce qui donne un temps $t = S \times v = 2$ heures pour peindre ces 4 murs. Par conséquent, il faudrait $\dfrac{2}{4} = 0,5$ heure à ce peintre moyen pour peindre un seul mur.

Autrement dit, si les 4 peintres peignaient un seul mur tous en même temps, cela leur prendrait une demi-heure. On aurait pu trouver ce résultat directement en calculant la moyenne harmonique des temps, qu’on aurait divisée par 4:

$\dfrac{1}{4} \times \dfrac{4}{\dfrac{1}{6} + \dfrac{1}{3} + \dfrac{1}{2} + \dfrac{1}{1}} = \dfrac{1}{\dfrac{2}{12} + \dfrac{4}{12} + \dfrac{6}{12} + \dfrac{12}{12}} = \dfrac{1}{\dfrac{24}{12}} = 0,5$

Ce qui est bien, c’est que ce genre de problème se multiplie à l’infini: par exemple, si une poule pond 1 œuf tous les 2 jours et une autre poule pond 1 œuf tous les 3 jours, en moyenne, combien d’œufs pondent-elle à elles deux par jour ?

Le problème des échelles qui se croisent

Voici un deuxième exemple amusant où intervient une moyenne harmonique. Deux échelles sont posées dans un couloir (devinez qui les a posées là ? Oui, c’est bien lui…). La première échelle touche le mur de gauche à une hauteur de 1,5 mètre. L’autre échelle touche le mur de droite à une hauteur de 2,5 mètre. A quelle hauteur les deux échelles se croisent-elles ?Il s’agit ici d’un problème géométrique, où donc se cache la moyenne harmonique me direz-vous ? Pour le découvrir, nous allons nous aider du théorème de Thalès et des notations suivantes: Dans le triangle $ABD$ , on a $\dfrac{NM}{AB} = \dfrac{DN}{DA}$ c’est-à-dire $\dfrac{h}{1,5} = \dfrac{\ell_2}{\ell}$ . Ainsi, $\ell_2 = \ell \times \dfrac{h}{1,5}$ .

De même dans le triangle $ACD$ , on a $\dfrac{NM}{CD} = \dfrac{AN}{AD}$ donc $\dfrac{h}{2,5} = \dfrac{\ell_1}{\ell}$ d’où $\ell_1 = \ell \times \dfrac{h}{2,5}$ .

Comme $\ell_1 + \ell_2 = \ell$ , on a donc $\ell \times \dfrac{h}{2,5} + \ell \times \dfrac{h}{1,5} = \ell$ . Par conséquent, $\dfrac{h}{2,5} + \dfrac{h}{1,5} = 1$ donc

$\boxed{ h = \dfrac{1}{\dfrac{1}{1,5} + \dfrac{1}{2,5}}}$

Autrement dit, la hauteur à laquelle se croisent les échelles est la moitié de la moyenne harmonique des hauteurs atteintes par les échelles sur les murs du couloir. Un simple calcul donne alors $h = 0,9375$ mètre.

D’autres moyennes ?

Outre les moyennes harmonique et arithmétique, il existe une troisième moyenne dont je n’ai pas parlé dans cet article, qu’on appelle moyenne géométrique. Vous ne la connaissez pas ? Ne m’obligez pas à écrire un article qui s’appellerait « Géométrique, trique, trique »…

Sources

La moyenne harmonique sur Wikipédia.
Le problème des échelles qui se croisent sur Wikipédia. En fait, ce problème est beaucoup plus difficile que la version donnée dans l’article: dans sa version initiale, les données de ce problème sont les longueurs des échelles (et non les hauteurs auxquelles elles touchent les murs) ainsi que la hauteur à laquelle elles se croisent et on demande de trouver la largeur du couloir.
Une vidéo en anglais pour comprendre le lien entre le problème des échelles et la moyenne harmonique.

8 commentaires pour Harmonique, nique, nique…

Celine dit :

21 octobre 2018 à 8 h 45 min

Merci,
J’ai beaucoup ri…

J’aimeJ’aime

Réponse
Anonyme dit :

21 octobre 2018 à 11 h 43 min

Une référence musicale a été oubliée :

Je suis déçu. 😉

J’aime bien la conclusion et je crois qu’il va falloir l’écrire cet article. 🙂

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  25 octobre 2018 à 21 h 35 min
  
  Puisque mes lecteurs me le demandent, je vais peut-être écrire cet article ! 😀
  
  J’aimeJ’aime
  
  Réponse
Anonyme dit :

24 octobre 2018 à 22 h 32 min

Il reste encore la moyenne quadratique ; en traçant deux segments [AB] et [BC] de longueurs respectives a et b, avec B sur [AC], on peut faire apparaître les quatre moyennes par des constructions géométriques, en plaçant le milieu de [AC], en construisant le point D à l’intersection d’un demi-cercle de diamètre [AC] et de la perpendiculaire à (AC) en B, et pour harmonique et quadratique je soupçonne l’utilisation de Thalès et de Pythagore respectivement (me rappelle plus).

J’aimeJ’aime

Réponse
Ping : Les moyens de moyenner | Automaths
Blacksheep dit :

31 décembre 2018 à 12 h 46 min

Très intéressant!
On attend la suite!

J’aimeJ’aime

Réponse
Anonyme dit :

24 juillet 2019 à 16 h 30 min

mon prof de math universitaire

a rezolu une matrice

le calcul final

était 0x=0

le prof a ecrit x=0

ce qui est totalment fo

x= ds les math ancienne version vo tout les nombres plus qu’un otre

dc il y a une incoherence

le prof de math universitaire est incoherent

0x=0

x=0/0 tout les ancienne math ca pose problem

de ce constat

g lu 30 000 site internet

un site proposait

de dire si

1/0 exyste alors 0phi=1 est vrai

tout en pensant qe c impossible

il dy c impossible

mais il m’a ouvert la voix a la vérité

0p=1 est vrai ds un nouvelle ensemble de nombre qui inclus les reel

les complexe inclus les reel

les complexe n’inclus pas les neo complexe et les neo complexe inclus pas les complexe tout deux inclus les reel

les super complexe inclus complexe et neo complex

les qaternion inclus les complexe
les neo qaternion inclus les neo complexe

neo qaternion et qaternion sont inclus ds les super qaternion

J’aimeJ’aime

Réponse
Anonyme dit :

24 juillet 2019 à 17 h 23 min

https://fr.wikipedia.org/wiki/%C3%89ponge_de_Menger
l’eponde de Mandelbrot
permet un processeur 3d et sa ventilation optimal pour right here right now

J’aimeJ’aime

Réponse