Un pentagone régulier est un polygone à cinq côtés tous de même longueur. Il est possible de construire un tel pentagone à l’aide de la règle (non graduée) et du compas, ce qui sera décrit ci-dessous. Notons qu’il n’est pas possible de construire tous les polygones réguliers à l’aide de la règle et du compas: en effet, de tels outils ne sont pas suffisant pour construire de manière exacte un heptagone (polygone régulier à sept côtés).
Cet article commence avec une proposition de méthode de construction d’un pentagone régulier , puis une justification mathématique de cette construction.
Voici une animation de la construction. Les différentes étapes sont décrites en-dessous.
Etapes de la construction:
- Tracer un cercle c de centre O, ainsi que deux diamètres perpendiculaires que nous nommerons
et
.
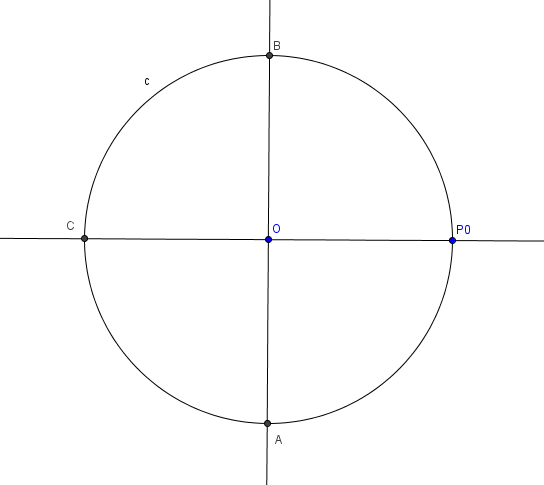
- Placer un point M au milieu de
, et, à l’aide du compas, tracer un arc de cercle centré en M, passant par B. Il coupe le segment
en D. (Remarque: la construction de M peut se faire en traçant la médiatrice de
au compas).

- Tracer la médiatrice de
(on note I le milieu de ce segment). Elle coupe le cercle c en
.

- Tracer le segment
et à l’aide du compas, reporter ce segment le long du cercle pour obtenir les points
, Puis relier les sommets du pentagone.
La construction est maintenant terminée !
Pourquoi cette construction marche ?
Après avoir fait un joli dessin, intéressons-nous un peu plus à la théorie mathématique qui prouve que ces étapes de construction nous donnent bel et bien un pentagone régulier. Le principe de cette construction est de placer 5 points régulièrement espacés sur un cercle, ce qui revient à couper le cercle en cinq parts égales. Puisqu’un tour complet vaut , le principe est donc de découper le cercle en cinq angles faisant chacun
radians. Dans toute la suite, et pour simplifier les explications, nous nous contenterons d’un cercle de rayon 1.
Mais alors, comment tracer un angle de radians ? Pour cela, on a besoin de construire un segment de longueur
. Plus généralement, si on sait construire un segment
de longueur
alors on sait construire un angle de
radians en traçant la perpendiculaire à
passant par I, comme le montre la figure ci-dessous (le rayon de ce cercle étant 1):

Toute la question de la construction d’un pentagone régulier se résume donc à la construction d’un segment de longueur . Il se trouve que ce nombre peut se calculer très simplement puisque
. Nous allons démontrer cette affirmation en utilisant des outils empruntés à l’algèbre:
- Posons
. On remarque immédiatement que
.
- Le nombre complexe
est une racine du polynôme
et comme
est différent de 1, ce même nombre vérifie la relation:
- Puisque
est non nul, on peut diviser la relation précédente par
ce qui donne (en regroupant les termes):
donc:
(car
c’est-à-dire
.
- Enfin, en divisant la dernière égalité par 4 et en utilisant le fait que
, on obtient finalement:
.
- Cela signifie que le nombre
est une racine du polynôme
. Or, d’après les formules bien connues, ce polynôme possède exactement deux racines à savoir:
et
.
Puisque (le cosinus d’un angle aigu est toujours positif !), c’est qu’on a nécessairement
. CQFD.
Pour terminer de justifier notre construction, il faut montrer que le segment que nous avons construit dans l’étape n°4 vaut bien
. Cela prouvera qu’effectivement l’angle
vaut
. Rappelons que nous avions pris
comme le milieu d’un rayon, ce qui donne donc
.
Comme (voir figure de l’étape 4), il est donc équivalent de montrer que
. Or,
. D’après le théorème de Pythagore,
, ce qui implique donc que
.
Nous sommes rassurés, nous avions bien construit un angle de !
A voir: Pour ceux qui souhaitent aussi apprendre à tracer un décagone, vous pouvez vous rendre sur cet autre article de ce blog: Tracer un décagone « pour les nuls ».




merci pour la technique
J’aimeJ’aime
De rien, et merci pour le petit commentaire 😉
J’aimeJ’aime
Merci
J’aimeJ’aime
De rien.
J’aimeJ’aime
il es tro maran ton commentair signer misi ben ladon (pas lardon hihihi ^^prout^^et jtdr les ptit oiseaus long et moux^^
J’aimeJ’aime
Interesting.
J’aimeJ’aime
Je
J’aimeJ’aime
moi je sais tu fait un point sur ta feuille preférence milieu,, si tu veut que les coté de ton pentagone fasse 5 cm par exemple,, tu fait 5 diviser par 1,25 = (4) donc du point tu trace un trai vers la droite horizontalement de 4 cm « ce trai que tu viens de faire on l’appel base » » reviens au point du debut et la tu fait un trai vers le bas de 3/4 (trois quart) la base c’est a dire 3 cm ensuite du point de dépard tu fait un grand trai vers le haut de 3 fois base c’est a dire de 12 cm ensuite tu relie les extremité et tu duplique la base a gauche pour obtenir la geometri de ton pentagone le point de depard prend le nom de Z en haut A a droite B en bas C et a gauche D,,, la longeur de Z’A et égale a douze cm tu fait 12 diviser par 10 fois 4 (4 dizieme) cela donne 4,8 tu part de Z puis tu suis la ligne vers le haut jusqu’a 4,8 cm et la tu trace une droite paralelle a la base c’est a dire horizontalement et la ton pentagone et fait et encore mieux de se point au sommet point A il reste 7,2 cm ben tu le divise en deux ca donne 3,6 cm et se 3,6 cm c’est le rayon de ton pentagone « » tu gomme les reste et redessine ton pentagone au propre et depuis le milieu de tes coté tu trace un trai bien droit de 3,6 cm et tu as ton point et tous ca sans compas
J’aimeJ’aime
pourquoi tu fais un truc trop long on a compris
J’aimeJ’aime
Incompréhensible. En suivant scrupuleusement vos indications, on arrive jusqu’à la ligne « à 4,8 de Z », mais vous n’en indiquez pas les extrémités. Du coup ça ne fait pas un pentagone tout ça. Merci de donner une description plus précise de la fin…
J’aimeJ’aime
à Sweet : Je doute que votre construction mène à un pentagone régulier. Les deux premiers côtés de votre pentagone sont construits en juxtaposant deux triangles rectangles de côtés 3,4,5 (au passage votre méthode impose une valeur 5 pour le côté). Donc l’angle entre les premiers côtés de votre pentagone et la radiale vaut arccos(3/5) = arccos(0,6). Mais dans le cas du pentagone régulier, le cosinus de l’angle correspondant vaut cos(3/5*pi/2) = 0,587. Cela ne fait pas un gros écart, le pentagone que vous obtenez ressemble à un pentagone régulier, mais cela n’en est pas un.
J’aimeJ’aime
à Sweet, j’ai enfin terminé votre figure, mais la fin de ce que vous indiquez est aussi fausse que le début. Vos valeurs magiques (3, 4, 5, puis 12 et 0,48) mènent de nouveau à des angles proches de ceux d’un pentagone régulier, mais faux. En particulier le demi-angle entre deux côtés opposés fait chez vous atan(4/12) = atan(0,333…) sur un pentagone régulier, on doit avoir tan(pi/10) = 0,324. Là encore, vous prenez les valeurs qui vous arrangent, mais ça ne fait pas un pentagone régulier.
J’aimeJ’aime
comment on la trace la médiatrice?
Dans quels paramètres?
J’aimeJ’aime
MERCI
J’aimeJ’aime
1 Carré : VOILA TOUT LES POLYGONE REGULIER
a) Si on connaît le côté AB , tracer en A et B les perpendiculaires à AB et porter AD = AB = BC
b) Si on dessine d’abord une circonférence , tracer deux droites « diamètres » perpendiculaires .
2 – Triangle équilatéral : INFO PLUS ! ! ! ! !
Si on connaît le côté AB , tracer les cercles des centres A et B et de rayon AB .
Si on trace d’abord une circonférence , porter 6 cordes consécutives égales au rayon du cercle et joindre les points comme l’indique la figure .
3 ) Hexagone régulier INFO PLUS ! ! ! !
a) Si on connaît le coté AB tracer les cercles de centres A et B et de rayon AB , puis le cercle de rayon OA et de centre O . Tracer à partir de A , 6 cordes consécutives égales à AB
b) Si on dessine d’abord une circonférence, porter 6 cordes consécutives égales au rayon du cercle.
Remarque importante : possibilités de tracés à partir d’un carré
En traçant l’axe de symétrie d’un côté ( exemple AB) du carré , on partage l’arc AB en deux parties égales.
En portant des cordes successives égales à MA ou MB , on forme un polygone régulier de 8 côtés ( octogone) . En faisant une construction analogue sur ce nouveau polygone , on tracerait un polygone régulier de 16 côtés .
Autre méthode :
Une autre construction possible : faire à partir de l’hexagone régulier permet de tracer un polygone régulier de 12 côtés ( dodécagone), puis de 24 côtés .
Troisième possibilité.
A partir d’un carré de centre O. Le carré A BCD , tracer les diagonales puis les cercles de centres A ; B ; C ; D et de rayons AO ; BO ; CO ; DO
4°) Dodécagone régulier (12 côtés) INFO PLUS ! ! ! !
Tracer deux diamètres perpendiculaires AB et CD .
De A ; B ; C , C décrire des arcs de cercles de rayon AO ; BO ; CO ; DO .
5°) Pentagone régulier: ( 5 côtés) INFO PLUS ! ! !
Tracer deux droites perpendiculaires , de diamètre AB et CD .
Déterminer M milieu de OD . Décrire le cercle de centre M et de rayon MA et déterminer E . Porter ensuite 5 cordes successives égales à AE à partir de A .
6°) Décagone régulier ( 10 côtés) INFO PLUS ! ! !
Sur la figure précédente , porter à partir de A , 10 cordes successives égales à OE ( voir OE ci dessus)
J’aimeJ’aime
Merci beaucoup !!!
J’aimeJ’aime
🙂
J’aimeJ’aime
Superbe explication !! =)
Dites moi, comment peut-on retrouver le nombre d’or (1.618033…….) a partir de ce pentacle svp ?
Merci.
J’aimeJ’aime
Merci 🙂
Le nombre d’or correspond à la distance CD sur la figure (dans le cas où le rayon du cercle est 1).
J’aimeJ’aime
ca ne marche pas! ;(
J’aimeJ’aime
La démonstration mathématique en fin d’article prouve qu’il est impossible que ça ne marche pas…
Soufflez et reprenez les étapes calmement.
J’aimeJ’aime
Cela fait bien un pentagone régulier mais comment lui donner les bonnes dimensions ?
( 6 cm )
J’aimeJ’aime
Moi non plus ca marche pas
J’aimeJ’aime
Merci j’ai ressayé et sa marche (réponse a Blog de maths le 25 juin à 15h22)
J’aimeJ’aime
Ben tu vois 🙂
J’aimeJ’aime
perso la première explication est de loin la pus simple . sur le terrain une ficelle et un mètre suffise
J’aimeJ’aime
Merci ! ! Y a-t-il un moyen de connaitre le rayon du cercle en partant des segment d’un pentagramme croisé, c-a-d trouver la mesure de OA à partir du segment P1P4 ?
J’aimeJ’aime
Merci! Ma prof de maths nous a demander de construire un pentagone régulier en devoir maison et d en faire une éolienne. C pour un petit concours. Encore merci!!!!
J’aimeJ’aime
Explication complète mais un peu compliquée 😉
Merci!!
J’aimeJ’aime
Pour améliorer l’animation, essaye de mettre un bouton « pause ll » , pour que ça soit plus facile :p
Merci encore pour ton explication 😀
J’aimeJ’aime
merci
J’aimeJ’aime
merci beaucoup pour toutes ses explications
J’aimeJ’aime
merci
J’aimeJ’aime
bonjour
pour vous amuser, ajoutez la 3D
cordialement
J’aimeJ’aime
Ma question paraitra sans doute ridicule mais vu mon niveau de maths je n’ai pas pu suivre la démonstration. Je me demande si lorsque je construit un pentagone régulier au compas, ily a une relation entre l’écart de mon compas au début et la longueur d’un côté du pentagone à la fin. En gros est ce que je peux choisir un écartement de compas précis pour que mon pentagone est des côtés de 3cm chacun.
Merci pour l’aide pour la construction en tout cas 🙂
J’aimeJ’aime
Ce n’est pas une question bête, et, en effet, il y a un lien entre le rayon du cercle et la longueur d’un côté du pentagone ! C’est une question que je n’ai pas traitée dans cet article mais il existe une formule (que je démontrerai peut-être si j’ai le temps un jour…):
Si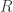 est le rayon du cercle (c’est-à-dire l’écartement de ton compas) alors, on peut montrer que la longueur
est le rayon du cercle (c’est-à-dire l’écartement de ton compas) alors, on peut montrer que la longueur  d’un côté du pentagone est donnée par la formule:
d’un côté du pentagone est donnée par la formule: 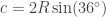 .
.
Donc, si tu as un écartement de 5cm sur ton compas, chaque côté du pentagone fera .
.
A l’inverse, si tu veux dessiner un pentagone de côté donné (par exemple, tu veux un pentagone de côté ) alors, on a la formule inverse:
) alors, on a la formule inverse:  et donc, il faudra prendre un écartement de
et donc, il faudra prendre un écartement de  .
.
J’aimeJ’aime
Merci pour votre aide
J’aimeJ’aime
Je voulais savoir si il était possible de trouver cet écartement sans graduation/calcul;
(En gros) Je veux faire un pentagone d’une longueur donner que je peux repoorter avec mon compas, comment devrait m’y prendre ?
J’aimeJ’aime
moi sa ne marche pas j’ai essayer 3 fois sa ne marche quelqu’un aurait une astuce pour mieux y arriver je vous précise que j’ai un côté AB de 7cm ???? AIDEEEEEE
J’aimeJ’aime
Bonjour, je me permets d’écrire pour vous signaler une erreur de mot… Vous dites dès l’introduction qu’il n’est pas possible de construire tous les pentagones réguliers avec une règle et un compas, et vous justifiez votre propos en donnant l’exemple de l’heptagone… Vous vouliez sans doute écrire polygones réguliers et non pentagones.
Bonne journée et merci pour vos explications.
J’aimeJ’aime
Tout à fait, il fallait bien lire « polygones » ! L’erreur a été rectifiée. Merci !
J’aimeJ’aime
Ping : 👍 comment faire ème
super
J’aimeJ’aime
merci beaucoup !
J’aimeJ’aime
Compliquer pour un sixième si vous pouviez le simplifier…
J’aimeJ’aime
La démonstration ne peut pas vraiment se simplifier, je me demande comment faire sans les notions de trigonométrie (cosinus), nombres complexes, et Pythagore.
Par contre la construction devrait être accessible, peut-être manque-t-il juste (notamment pour un sixième) l’explication de comment construire la médiatrice de deux points (disons A et B).
Placer le compas en A et prendre un écartement assez grand (supérieur à AB/2), tracer le cercle de centre A, et celui de centre B de même rayon. Les deux cercles se coupent en deux points, les relier, on a la médiatrice de [AB].
Une fois compris, il n’est pas nécessaire de tracer les cercles en entiers, juste des petits arcs.
Ainsi on peut facilement avoir le milieu d’un segment (la médiatrice de [AB] le coupe en son milieu).
C’est un peu long à expliquer mais pas bien compliqué.
J’aimeJ’aime
Voici une preuve sans trigonométrie et sans nombres complexes, mais c’est une construction différente (ma préférée).
http://maths.ac-noumea.nc/polyhedr/polyg_draw.htm#penta
J’aimeJ’aime
J’avais oublié mes feuilles de théorie 😂
J’aimeJ’aime
Bonjour,
Pour construire un polygone régulier il ne me paraît pas judicieux de construire un côté puis de le reporter sur le cercle circonscrit : en pratique on retombe rarement sur le point de départ, même avec un crayon bien taillé !
Parmi les constructions possibles, je pense qu’il convient de privilégier celle qui fournit tous les sommets sans reports de la longueur d’un côté.
Exemples : http://maths.ac-noumea.nc/polyhedr/polyg_draw.htm
Bien cordialement, Maurice
J’aimeJ’aime
Ping : Comment ne pas tracer un heptagone régulier ? | Blogdemaths
merci!!
J’aimeJ’aime
Ping : Gâteau ballon de foot : chocolat, praliné, vanille - Sucre d'Orge et Pain d'Epices
y a quelque chose pour les 6e?
J’aimeJ’aime
Je ne connais pas les programmes actuels, mais je pense qu’en sixième il convient surtout d’apprendre à utiliser la règle et le compas (l’équerre n’est pas un instrument de construction !) et de comprendre ce qu’est une construction : créer de nouveaux points comme intersections de droites et de cercles.
On peut évidemment faire reproduire des constructions simples (triangle équilatéral, hexagone, carré et octogone,rosaces…) à partir d’un texte ; l’inverse est évidemment aussi intéressant (décrire une construction). Mais ce n’est qu’en cinquième que je commençais à insister sur la nécessité de prouver ; justifier une construction est une approche intéressante de la démonstration.
J’aimeJ’aime
montre moi tres biens
J’aimeJ’aime
C’est bientôt Noël, j’ai 70 ans et j’ai oublié comment on fait une étoile à 5 branches. Plus-tôt que d’aller voir sur internet, je fais un cercle de par ex 10cm de rayon j’ajoute a mon compas 1/5, soit 2cm, je reporte sur le cercle en partant d’un point «A» 5x les 12cm j’arrive au point B.
Je mesure la distance entre le point A et le B « Y » je divise Y par 5 et je l’ajoute au 12 cm.
Je reprends un point de départ C et je reporte 5x (12+Y/5) j’arrive au point D.
Si j’estime la distance entre C et D trop grande, je recommence l’opération en ajoutant 1/5 de la distance entre C et D.
Ce n’est pas scientifique, mais pour faire un dessin c’est suffisant
J’aimeJ’aime
C’est un bon bricolage. Attention ! il n’y a dans mon esprit rien de négatif dans « bricolage » :c’est une méthode qui permet à un non spécialiste de résoudre un problème de façon satisfaisante pour ses besoins.Un bon bricoleur fait souvent preuve d’imagination et d’inventivité… juste ce qu’il faut pour se lancer en mathématiques.
Cette méthode par approximations successives a un grand avantage : elle permet de dessiner n’importe quel polygone régulier, même ceux qui ne sont pas constructibles à la règle et au compas ! Je l’ajoute donc sur la page internet que je consacre à ce sujet :
http://maths.ac-noumea.nc/polyhedr/polyg_draw.htm
Quand il en existe une, une construction simple reste cependant plus efficace et plus précise..
J’aimeJ’aime
Et en pliage: tu prends une bande de papier et tu fais un noeud simple sans (trop) serrer. Je laisse la démonstration à ceux que cela tente…
J’aimeJ’aime
Je serais ravir de service car je crois que j ai encore besuons
J’aimeJ’aime
Je serais ravir de service car je crois que j ai encore besuons
J’aimeJ’aime
Toute la question de la construction d’un pentagone régulier se résume donc à la construction d’un segment de longueur cos(\frac{2\pi}{5}). Il se trouve que ce nombre peut se calculer très simplement puisque cos(\frac{2\pi}{5}) = \frac{-1 + \sqrt{5}}{4}. Nous allons démontrer cette affirmation en utilisant des outils empruntés à l’algèbre:
Posons z=e^{\frac{i2\pi}{5}}. On remarque immédiatement que cos(\frac{2\pi}{5})=Re(z)=\frac{z+\bar{z}}{2}=\frac{z+\frac{1}{z}}{2}.
Le nombre complexe z est une racine du polynôme X^5-1 = (X-1) (X^4 + X^3 + X^2+X+1) et comme z est différent de 1, ce même nombre vérifie la relation:
z^4 + z^3 + z^2+ z+1 = 0
Puisque z est non nul, on peut diviser la relation précédente par z^2 ce qui donne (en regroupant les termes):
(z^2+\frac{1}{z^2}) + (z+\frac{1}{z}) + 1 = 0
donc:
(z+\frac{1}{z})^2 – 2 + (z+\frac{1}{z}) + 1 = 0 (car a^2+b^2=(a+b)^2-2ab) c’est-à-dire
(z+\frac{1}{z})^2+(z+\frac{1}{z})-1=0.
Enfin, en divisant la dernière égalité par 4 et en utilisant le fait que cos(\frac{2\pi}{5}) = \frac{z+\frac{1}{z}}{2}, on obtient finalement:
cos(\frac{2\pi}{5})^2+\frac{1}{2}cos(\frac{2\pi}{5})-\frac{1}{4}=0.
Cela signifie que le nombre cos(\frac{2\pi}{5}) est une racine du polynôme X^2+\frac{1}{2}X-\frac{1}{4}. Or, d’après les formules bien connues, ce polynôme possède exactement deux racines à savoir:
X_1=\frac{-1+\sqrt{5}}{4} >0 et X_2=\frac{-1-\sqrt{5}}{4} 0 (le cosinus d’un angle aigu est toujours positif !), c’est qu’on a nécessairement cos(\frac{2\pi}{5})= X_1 = \frac{-1+\sqrt{5}}{4}. CQFD.
Pour terminer de justifier notre construction, il faut montrer que le segment [OI] que nous avons construit dans l’étape n°4 vaut bien \frac{-1+\sqrt{5}}{4}. Cela prouvera qu’effectivement l’angle P_1OP_0 vaut \frac{2\pi}{5}. Rappelons que nous avions pris M comme le milieu d’un rayon, ce qui donne donc OM=\frac{1}{2}.
Comme OI= \frac{OD}{2} (voir figure de l’étape 4), il est donc équivalent de montrer que OD = \frac{-1+\sqrt{5}}{2}. Or, OD = DM -OM = BM – OM. D’après le théorème de Pythagore, BM=\sqrt{1^2 + (\frac{1}{2})^2} = \frac{\sqrt{5}}{2}, ce qui implique donc que OD = \frac{\sqrt{5}}{2} – \frac{1}{2} = \frac{-1+\sqrt{5}}{2}.
Nous sommes rassurés, nous avions bien construit un angle de \frac{2\pi}{5} !
J’aimeJ’aime
Ping : Sandwich cake ballon de foot | Mamou & Co
Merci pour la méthode
J’aimeJ’aime
Je n’ai pas réussi à tracer ce que je voulais car vos informations ne me donnent pas la même longueur pour tous les côtés.
J’aimeJ’aime
Mercie pour les 4 technique .je n’avais pas compris en classe mais grâce à vous jai très b1 cmpris.
J’aimeJ’aime
Explications claires et précise,
parfait pour réaliser un pentagone quand on ne sait pas comment s’y prendre, merci.
J’aimeJ’aime
Merci et bravo pour cette démonstration, très didactique. On pourrait regretter que la démonstration de la relation cos(2pi/5)=(-1+V5)/2 par l’algèbre des nombres complexes semble sortir du chapeau (en particulier la factorisation du polynôme z4+z3+z2+z+1). Mais c’est probablement un choix pour ne pas alourdir l’article et éviter de faire appel à des notions plus avancées sur la géométrie dans le plan complexe (identité d’Euler, etc)
Si on observe dès le départ que le cercle unité de R2 est un analogue du cercle unité C du plan complexe, on peut utiliser directement les propriétés de ce dernier : on peut associer à tout pentagone régulier à N points une suite Zj de C (j=0…N-1) telle que Zj a pour argument 2jpi. Ces Zj ont les propriétés suivantes : Zj = 1/Zj*, Zj^N = 1 et Zj = ZN-j*
Partant de là, la factorisation de Z^5-1 est immédiate, de même que l’identification des coefficients de la forme canonique et le calcul des cosinus. Mais j’imagine que vous avez voulu faire court pour éviter de perdre une trop grande partie de vos lecteurs ! Bel article en tous cas !!
J’aimeJ’aime
erratum : à la fin du deuxième paragraphe ci-dessus, lire : « telle que Zj a pour argument 2jpi/N »
J’aimeJ’aime