Séries géométriques, géométriquement !

Publié le 17 avril 2016 par blogdemaths

Prenez un nombre $x$ (disons positif), et formez la somme de toutes les puissances de $x$ :

$x^0 + x^1 + x^2 + x^3 + \cdots + x^n + \cdots$

Vous calculez alors ce qu’on appelle la somme de la série géométrique de raison $x$ . Par exemple, la somme de la série géométrique de raison $x=\frac12$ , est:

$1 + \dfrac12 + \dfrac14 + \dfrac18 + \cdots + \dfrac{1}{2^n} + \cdots$

Les séries géométriques sont connues depuis très longtemps et apparaissent un peu partout en mathématiques (par exemple, pour montrer que tôt ou tard vous gagnerez au Loto !). En fait, on les connaît tellement bien qu’on sait même calculer leur somme. En effet, on peut montrer que pour $0 \leqslant x <1$ :

$\boxed{ 1+x+x^2 + \cdots + x^n + \cdots = \dfrac{1}{1-x} }$

(En fait, cette formule est valable même pour $-1<x<1$ , mais nous ne nous occuperons pas des $x$ négatifs dans cet article. Et si $x \geqslant 1$ ? la somme tend grossièrement vers $+\infty$ , donc nous ne nous en occuperons pas non plus…)

Tout ça est bien beau mais comment prouver cette formule pour les séries géométriques ? Eh bien, grâce à de la géométrie ! (ce qui est quand même la moindre des choses, vu leur nom…)

Le cas 1/2

Commençons par un cas particulier, celui de la somme de la série géométrique de raison $x=\frac12$ . Si on en croit la formule précédente, nous devrions trouver que:

$1 + \dfrac12 + \dfrac14 + \dfrac{1}{8}\cdots = \dfrac{1}{1-\frac12}=2$

Voyons voir comment montrer géométriquement cette égalité. Pour cela, commençons par considérer un carré de côté 1. Ce carré a donc pour aire totale 1:Coupons ce carré en deux:
L’aire en rouge vaut donc $\frac12$ . Coupons à nouveau en deux la partie restante en blanc:Comme l’aire en blanc valait $\frac12$ à l’étape précédente, quand on la coupe en deux, elle devient $\frac12 \times \frac12 =\frac14$ . On recommence ainsi de suite, et on coupe en deux à chaque fois la partie restante: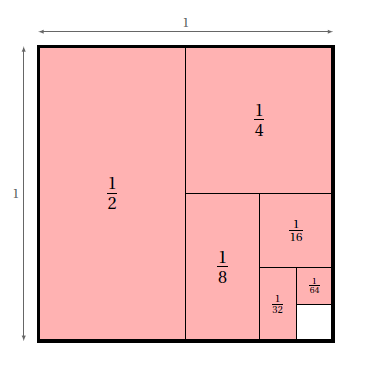Si on découpe indéfiniment le carré, nous voyons que l’aire totale en rouge sera de $\frac12 + \frac14 + \frac18 + \cdots$ Comme cette aire en rouge va remplir tout le carré (qui a pour aire 1, rappelons-le), on peut affirmer que:

$\dfrac12 + \dfrac14 + \dfrac18 + \cdots = 1$

et donc :

$1 + \dfrac12 + \dfrac14 + \dfrac18 + \cdots = 2$

Joli, n’est-ce pas ? Mais inutile… car cette démonstration, aussi élégante soit-elle, ne se généralise pas très bien au cas d’une série géométrique de raison $x$ quelconque (essayez par exemple de couper le carré en 3 à chaque étape, vous verrez que vous ne remplirez jamais tout le carré…). Certes, il existe des découpages du carré qui permettent de prouver la formule dans le cas général (voir figure ci-dessous) mais, hormis pour $x=\frac14$ , je ne les trouve pas géométriquement très parlants (si tant est que cette phrase ait un sens… et si tant ait que vous partagiez mon opinion !).

Source: https://www.maa.org/sites/default/files/Ajose61740393.pdf
Je ne sais pas pour vous, mais la figure de droite ne me parle pas du tout…

Je vous ai quand même promis une preuve géométrique en début d’article (oui, je vends du rêve !), donc il va falloir trouver autre chose. On va changer de stratégie: au lieu d’utiliser la notion d’aire, nous allons plutôt utiliser la notion de distance.

Une figure étrange…

Voici la figure que nous allons utiliser pour déterminer la somme de la série géométrique de raison $x$ :

Si vous n’êtes pas convaincu que cette figure permettra bel et bien de calculer la somme $1+x+x^2 + \cdots$ , attendez de voir la suite…

Expliquons tout de même comment construire cette figure: tracez un segment horizontal [OA] de longueur 1, puis, à partir de A, construisez un segment vertical [AB] de longueur $x$ (où $x$ représente la raison de notre série géométrique). Vous obtenez donc un triangle OAB rectangle en A. Ensuite, à partir de A, prolongez le segment [OA] en un segment [AC] de longueur 1. Et à partir de C, tracez un segment vertical [CD] de longueur 1 lui aussi:

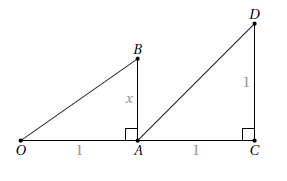
A partir de là, prolongez les demi-droites [OB) et [AD). Elles se coupent en un point P. Le point N est défini alors comme le pied de la perpendiculaire à (OA) passant par P:

(Remarque: vous comprenez sans doute à ce moment-là que les demi-droites [OB) et [AD) ne se coupent en un point P que si $x<1$ ; je vous laisse méditer là-dessus pour le moment…)

Il se trouve alors que le triangle APN est isocèle. Si vous voulez vous en convaincre, un petit coup de théorème de Thalès donne $\frac{AC}{AN}= \frac{CD}{PN}$ c’est-à-dire $\frac{1}{AN}=\frac{1}{PN}$ donc $AN=PN$ .

Quel est l’intérêt de cette figure ?

Si on était dans un repère, on dirait que la droite (OP) a pour coefficient directeur $x$ et que la droite (AP) a pour coefficient directeur 1.

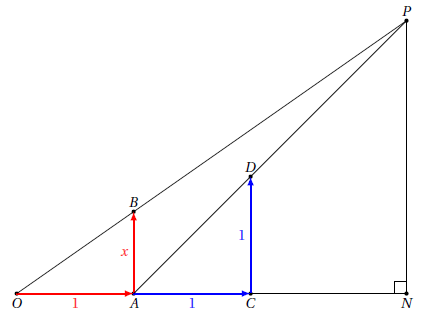
series_geometrique_demonstration_par_les_distances_fig_4_intepretation_coefficient_directeur

Vous vous souvenez peut-être qu’au collège, votre prof vous a dit que pour trouver graphiquement le coefficient directeur d’une droite, il faut partir d’un point de cette droite, se décaler d’une unité horizontalement vers la droite et alors la distance (algébrique, c’est-à-dire positive ou négative) qu’il faut parcourir verticalement pour retomber sur la droite est le coefficient directeur.

On en déduit la propriété suivante:

Propriété 1: Si on part d’un point de la droite (OP) et qu’on se déplace horizontalement d’une distance $y$ , alors il faut se déplacer verticalement d’une distance $y \times x$ pour revenir sur cette droite.

Dans un repère, cette propriété peut se comprendre de la façon suivante: puisque la droite (OP) a pour coefficient directeur $x$ , un vecteur directeur de cette droite est $\begin{pmatrix} 1 \\ x\\ \end{pmatrix}$ donc pour tout $y$ non nul , le vecteur $y \times \begin{pmatrix} 1 \\ x\\ \end{pmatrix} = \begin{pmatrix} y \\ y \times x\\ \end{pmatrix}$ est aussi un vecteur directeur de cette droite.

On a une propriété équivalente pour l’autre droite:

Propriété 2: Si on part d’un point de la droite (AP) et qu’on se déplace verticalement d’une distance $y$ , alors il faut se déplacer horizontalement d’une distance $y$ pour revenir sur cette droite.

Voilà, avec tout cela, nous sommes prêts à démontrer la formule sur la somme de la série géométrique de raison $x$ .

La démonstration tant attendue…

Pour démontrer la formule à partir de cette figure, nous allons faire une petite balade… nous allons partir du point O pour arriver au point P de la façon suivante:

Étape 1: On part de O et on se déplace horizontalement de 1 unité.

Étape 2: On se déplace ensuite verticalement jusqu’à revenir sur la droite (OP). Puisqu’on était parti de cette droite à l’étape précédente et qu’on s’était déplacé de 1 unité, la propriété 1 précédente nous dit qu’il faut se déplacer de $1 \times x = x$ unités pour retomber sur la droite.

Etape 3: On se déplace ensuite horizontalement jusqu’à atteindre la droite (AP). Mais puisqu’à l’étape précédente nous étions partis de cette même droite (AP) et que nous nous étions déplacés de $x$ unités verticalement, alors la propriété 2 nous dit que pour rejoindre (AP), il faut se déplacer de $x$ unités horizontalement également.

Etape 4: On se déplace verticalement jusqu’à rejoindre la droite (OP). Puisqu’à l’étape précédente on s’était déplacé horizontalement de $x$ unités horizontalement, la propriété 1 nous dit que pour rejoindre (OP), il faut se déplacer de $x\times x = x^2$ unités verticalement.

Etape 5: On se déplace horizontalement de façon à rejoindre la droite (AP). Comme à l’étape précédente on s’était déplacé de $x^2$ verticalement en partant de (AP), la propriété 2 nous dit qu’il faut aussi se déplacer horizontalement de $x^2$ pour rejoindre cette droite:

Bon, inutile de faire plus d’étapes, je pense que vous avez compris le principe. Voici la belle figure obtenue lorsqu’on répète indéfiniment ces déplacements: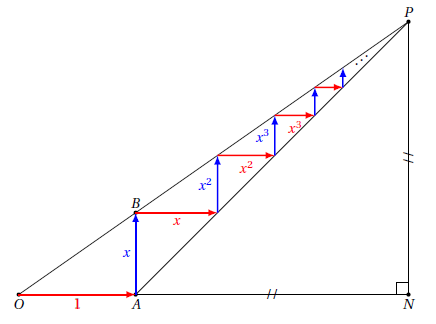

Intéressons-nous à présent à la distance totale parcourue horizontalement: lorsqu’on s’est déplacé de O à P, la distance qu’on a balayée horizontalement est

$1+x+x^2+x^3 + \cdots + x^n + \cdots$

Il s’agit de la somme des distances de tous les segments en rouge sur la figure précédente. Mais, le déplacement horizontal total effectué quand on va de O à P est aussi égal à la longueur du segment [ON], d’où:

$1+x+x^2+x^3 + \cdots + x^n + \cdots = ON$

Il nous faut donc déterminer la distance ON. Pour cela, reprenons notre configuration de départ:D’après le théorème de Thalès, on a:

$\dfrac{OA}{ON} = \dfrac{AB}{PN} \Rightarrow \dfrac{1}{ON} = \dfrac{x}{PN}$

mais comme $PN = AN = ON-OA= ON-1$ , on en déduit que:

$\dfrac{1}{ON} = \dfrac{x}{ON-1}$

donc: $ON \times x = ON-1$ , c’est-à-dire $1 = ON (1-x)$ d’où:

$\boxed{ON = \dfrac{1}{1-x}}$

ce qui prouve bien que $1+x+x^2+x^3 + \cdots + x^n + \cdots = \dfrac{1}{1-x}$ .

Source:

Cette image dont je ne sais même pas de quel bouquin elle est extraite ! N’hésitez pas à me le dire si vous le savez…

(Finalement, la référence a été trouvée et elle a été donnée par « none » dans les commentaires)

Ajout:

Il y a quand même une chose que l’on a affirmée dans cette démonstration et qui mérite qu’on s’y attarde un peu: c’est l’égalité $1+x+x^2+\cdots+x^n+\cdots=ON$ (qui signifie que quand on part du point O, on arrive bien au point P et on ne s’arrête pas avant). Pour la prouver, nous allons évaluer la différence $ON- (1+x+x^2+\cdots+x^n)$ , qu’on appelle reste partiel: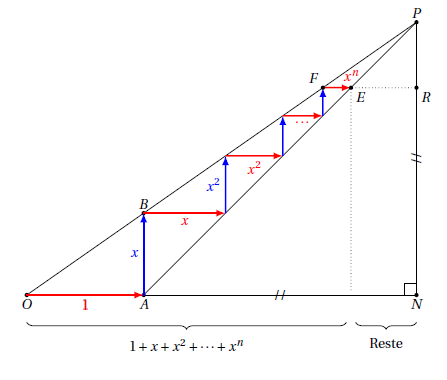Ce reste partiel correspond à la distance RE sur la figure. D’après le théorème de Thalès appliqué au triangle PAN, on a:

$\dfrac{PE}{PA}=\dfrac{RE}{AN}$

Mais d’après le théorème de Thalès appliqué cette fois-ci au triangle POA, on a:

$\dfrac{PE}{PA}=\dfrac{EF}{OA} \Rightarrow \dfrac{PE}{PA}=\dfrac{x^n}{1}$

On en déduit que $\dfrac{RE}{AN} = \dfrac{x^n}{1}$ , et donc, le reste partiel de cette série vaut : $RE = x^n \times AN$ . Comme la suite $(x^n)$ tend vers 0, cela veut bien dire que $1+x+x^2+\cdots+x^n+\cdots=ON$ .

Bonus (quand y en a plus, ben y en a encore): Comme $ON- (1+x+x^2+\cdots+x^n) =RE$ on en déduit que:

$1+x+x^2+\cdots+x^n = ON - RE = ON - x^n\times AN = ON - x^n (ON-1)$

donc:

$1+x+x^2+\cdots+x^n = ON (1-x^n) + x^n$

Or, on a vu que $ON = \dfrac{1}{1-x}$ , donc

$1+x+x^2+\cdots+x^n = \dfrac{1-x^n}{1-x} + x^n$

ce qui donne la formule bien connue de la somme partielle d’une série géométrique:

$\boxed{ 1+x+x^2+\cdots+x^n = \dfrac{1-x^{n+1}}{1-x} }$

Cet article, publié dans Géométrie, est tagué aire, balade, coefficient directeur, démonstration, distance, série géométrique, Thalès. Ajoutez ce permalien à vos favoris.

19 commentaires pour Séries géométriques, géométriquement !

Anonyme dit :

17 avril 2016 à 11 h 17 min

C’est très élégant et joli mais est-ce une preuve ?

J’aimeJ’aime

Réponse
- projetmbc dit :
  
  17 avril 2016 à 12 h 36 min
  
  C’est une base visuelle suffisante pour une preuve rigoureuse.
  
  J’aimeJ’aime
  
  Réponse
  - projetmbc dit :
    
    17 avril 2016 à 13 h 06 min
    
    En fait, il faudrait arriver à démontrer que la distance horizontale restant à droite va tendre vers zéro. Le problème serait de faire cela sans utiliser la somme des terme d’une suite géométrique.
    
    Au final, ce n’est pas immédiat me semble-t-il.
    
    J’aimeJ’aime
    
    Réponse
    - blogdemaths dit :
      
      17 avril 2016 à 15 h 43 min
      
      En effet, ce qu’on a admis implicitement dans l’article, c’est que $1+x+x^2+\cdots+x^n$ tend vers ON. Pour montrer cela, on peut déterminer la valeur de la distance restante à savoir:
      
      $ON - (1+x+x^2 + \cdots + x^n)$ .
      
      En fait, comme écrit dans la petite image à la fin de l’article, on peut montrer avec une double utilisation de Thalès que :
      
      $ON - (1+x+x^2 + \cdots + x^n) = AN \times x^n$
      
      ce qui, puisque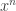 $x^n$ tend vers 0, prouve bien que la série géométrique converge vers ON ! (Si ce n’est pas clair pourquoi cette égalité est vraie, j’éditerai mon article pour expliquer cela…)
      
      J’aimeJ’aime
    - projetmbc dit :
      
      17 avril 2016 à 21 h 40 min
      
      Supers les compléments !
      
      J’aimeJ’aime
    - projetmbc dit :
      
      17 avril 2016 à 22 h 01 min
      
      Question complémentaire.
      
      Pour la limite nulle de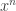 $x^n$ pour $-1 < x 1$ via l’inégalité de Bernoulli.
      
      Mais quelqu’un connait-il une preuve plus « élémentaire » ?
      
      J’aimeJ’aime
  - projetmbc dit :
    
    17 avril 2016 à 13 h 48 min
    
    On pourrait le faire par l’absurde.
    
    Si la distance restante ne tend pas vers $0$ , on note $m$ la borne inf des distances restantes. Par hypothèse, $m > 0$ .
    
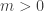    Dans ce cas, la suite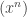 $(x^n)$ serait minorer par un réel non nul. Ceci n’est pas possible.
    
    J’aimeJ’aime
    
    Réponse
projetmbc dit :

17 avril 2016 à 12 h 39 min

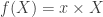Cette preuve n’est autre qu’un diagramme par escargot de $u_{n+1} = f(u_n)$ avec $f(X) = x\times X$ . C’est une très joli mais est-ce facile à trouver ? La première série de figures pour la somme des puissances de $\frac{1}{2}$ sont par exemple immédiates à imaginer.

J’aimeJ’aime

Réponse
- projetmbc dit :
  
  17 avril 2016 à 12 h 49 min
  
  Ne pas hésiter à corriger mon post ci-dessus qui a été publié trop tôt par erreur…
  
  J’aimeJ’aime
  
  Réponse
  - blogdemaths dit :
    
    17 avril 2016 à 15 h 11 min
    
    C’est fait !
    
    J’aimeJ’aime
    
    Réponse
    - projetmbc dit :
      
      17 avril 2016 à 21 h 32 min
      
      Merci.
      
      J’aimeJ’aime
none dit :

17 avril 2016 à 12 h 56 min

Il s’agit de « The Introduction to Infinite Series », W. J. Dobbs, The Mathematical Gazette
Vol. 9, No. 135 (May, 1918), pp. 242-246.
http://www.jstor.org/stable/3605310 et disponible chez vos dealers de PDF préférés.

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  17 avril 2016 à 15 h 18 min
  
  Merci pour cette référence ! Heureusement que je peux compter sur mes lecteurs, car je n’avais aucune idée d’où ce texte provenait 😉
  
  J’aimeJ’aime
  
  Réponse
Ping : un aire, la partie restant | Colours in Black and White
Roland Dassonval dit :

21 avril 2016 à 11 h 21 min

Merci pour l’idée !
Que j’ai reprise dans ce programme en test pour les amateurs…
http://rdassonval.free.fr/flash/suitegeometrique0.swf

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  5 mai 2016 à 17 h 04 min
  
  Joli 🙂
  
  J’aimeJ’aime
  
  Réponse
Paul A. Martel dit :

23 avril 2016 à 13 h 17 min

Dorénavant,y aurait-il possibiité de lire l’article (et tous les autes à venir) sous format pdf.

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  23 avril 2016 à 21 h 01 min
  
  Ce n’est malheureusement techniquement pas possible à l’heure actuelle.
  
  J’aimeJ’aime
  
  Réponse
Quang-Thai Ngo dit :

24 février 2017 à 4 h 30 min

Bonjour,

J’ai réalisé une vidéo en m’inspirant de votre article : https://www.youtube.com/watch?v=AA2DIgWL81o

Ma figure est un peu modifiée pour pouvoir utiliser les triangles semblables.

J’aimeJ’aime

Réponse