GaBuZoMeu…GaBuZoMeu

Dans la numération Shadok, il n’y a que quatre chiffres: Ga (zéro), Bu (un), Zo (deux) et Meu (trois). Tous les nombres sont alors fabriqués à partir de ces quatre chiffres selon un système de numération par position: autrement dit, les Shadoks comptent en base 4. Par exemple, le nombre ZoBuMeu vaut $2 \times 4^2 + 1 \times 4^1 + 3 \times 4^0 = 39$ .

Tout cela est beaucoup mieux expliqué (et surtout de manière beaucoup plus drôle) par les Shadoks eux-mêmes dans la (courte) vidéo ci-dessous:

Ce que nous allons voir dans cet article, c’est que les nombres:

GaBuZoMeu
GaBuZoMeuGaBuZoMeu
GaBuZoMeuGaBuZoMeuGaBuZoMeu
etc.
GaBuZoMeuGaBuZoMeuGaBuZoMeu…GaBuZoMeu (où GaBuZoMeu est répété $n$ fois)

renferment quelques propriétés insoupçonnées !

Ga) Des exemples pour commencer

Le nombre GaBuZoMeu signifie dans notre système décimal

$0 \times 4^3 + 1 \times 4^2 + 2 \times 4^1 + 3 \times 4^0 = 27$

La décomposition de GaBuZoMeu en produit de facteurs premiers est donc GaBuZoMeu = $3^3$ . De même, GaBuZoMeuGaBuZoMeu vaut

$0 \times 4^7 + 1 \times 4^6 + 3 \times 4^5 + 4 \times 4^4 + 0 \times 4^3 + 1 \times 4^2 + 3 \times 4^1 + 4 \times 4^0 = 6939$

et sa décomposition en produit de facteurs premiers est $3^3 \times 257$ .

Vous avez sans doute deviné le principe: on va décomposer les nombres GaBuZoMeuGaBuZoMeu…GaBuZoMeu (où GaBuZoMeu est répété $n$ fois) en produit de facteurs premiers puis voir ce qui se passe…

Bu) Une conjecture

Voici donc les résultats obtenus pour les premières valeurs de $n$ :

$\begin{array}{|r|r|r|} \hline n & \text{ GaBuZoMeu...GaBuZoMeu en base 10} & \text{ D\'ecomposition en facteurs premiers} \\ \hline 1 & 27 & 3^3 \\ 2 & 6 \, 939 & 3^3 \times 257 \\ 3 & 1 \, 776 \, 411 & 3^4 \times 7 \times 13 \times 241\\ 4 & 454 \, 761 \, 243 & 3^3 \times 257 \times 65537\\ 5 & 116 \, 418 \, 878 \, 235 & 3^3 \times 5 \times 11 \times 31 \times 41 \times 61681 \\ 6 & 29 \, 803 \, 232 \, 828 \, 187 & 3^4 \times 7 \times 13 \times 97 \times 241 \times 257 \times 673 \\ 7 & 7 \, 629 \, 627 \, 604 \, 015 \, 899 & 3^3 \times 29 \times 43 \times 113 \times 127 \times 15 790321 \\ \hline \end{array}$

On remarque que la décomposition en facteurs premiers des nombres GaBuzoMeu…GaBuZoMeu est assez particulière: elle semble toujours commencer par une puissance de 3 et tous les autres facteurs premiers apparaissent à la puissance 1.

Par exemple, le nombre GaBuZoMeuGaBuZoMeuGaBuZoMeu = $3^4 \times 7 \times 13 \times 241$ ne possède aucun facteur premier à une puissance supérieure ou égale à 2 (hormis 3 bien entendu) car $7$ , $13$ et $241$ apparaissent à la puissance 1. Voici donc la conjecture que l’on peut émettre:

[Conjecture]
La décomposition en produit de facteurs premiers du nombre GaBuZoMeu…GaBuZoMeu est le produit d’une puissance de 3 avec un nombre sans facteurs carrés.

Autrement dit, cette conjecture dit que si le nombre GaBuZoMeu…GaBuZoMeu est divisible par un nombre $p>3$ alors il n’est pas divisible par $p^2$ .

Avant de lire la suite, vous pouvez peut-être essayer de trouver un contre-exemple à cette conjecture (mais sachez qu’elle est vérifiée au moins jusqu’à $n=10$ …).

Zo) Expression générale du nombre GaBuZoMeu…GaBuZoMeu

Afin de prouver ou d’infirmer notre conjecture, nous allons essayer de donner une expression du nombre $N$ = GaBuZoMeu…GaBuZoMeu ( $n$ fois). Pour cela, nous allons devoir manipuler quelques sommes. Si cela est beaucoup trop indigeste pour vous, vous pouvez directement passer à la section suivante.

Tout d’abord, par définition même du nombre $N$ = GaBuZoMeu…GaBuZoMeu,

$\displaystyle N = \sum_{k=0}^{n-1} 0 \times 4^{3 + 4k} + 1 \times 4^{2+ 4k} + 2 \times 4^{1+ 4k} + 3 \times 4^{0+4k}$

Ainsi,

$\begin{array}{lcl} N & = & \displaystyle 0 \times \sum_{k=0}^{n-1} 4^3 \times 4^{4k} + 1 \times \sum_{k=0}^{n-1} 4^2 \times 4^{4k} + 2 \times \sum_{k=0}^{n-1} 4^1 \times 4^{4k} + 3 \times \sum_{k=0}^{n-1} 4^0 \times 4^{4k}\\[10pt] & = & \displaystyle 0 \times 4^3 \times \sum_{k=0}^{n-1} 4^{4k} + 1 \times 4^2 \times \sum_{k=0}^{n-1} 4^{4k} + 2 \times 4^1 \times \sum_{k=0}^{n-1} 4^{4k} + 3 \times 4^0 \times \sum_{k=0}^{n-1} 4^{4k}\\[10pt] & = & \displaystyle 0 \times \sum_{k=0}^{n-1} 4^{4k} + 16 \times \sum_{k=0}^{n-1} 4^{4k} + 8 \times \sum_{k=0}^{n-1} 4^{4k} + 3 \times \sum_{k=0}^{n-1} 4^{4k} \\[10pt] & = & \displaystyle 27 \times \sum_{k=0}^{n-1} 4^{4k} \\[10pt] & = & \displaystyle 27 \sum_{k=0}^{n-1} {\left(2^8\right)}^{k} \\[10pt] \end{array}$

Pour finir, on applique la fameuse formule sur la somme des termes d’une suite géométrique (un classique !) pour obtenir

$N = 27 \times \dfrac{ \left(2^8\right)^n - 1}{2^8 - 1} = \dfrac{27 ( 2^{8n} - 1)}{255}= \dfrac{9 (2^{8n}-1)}{85}$

Finalement le nombre $N$ = GaBuZoMeu…GaBuZoMeu ( $n$ fois) est égal à:

$\boxed{N= \dfrac{ 3^2 ( 2^{8n} - 1)}{5 \times 17} }$

Nous sommes encore loin d’avoir prouvé ou infirmé notre conjecture, mais, tout de même, cette formule nous montre que les nombres GaBuZoMeu…GaBuZoMeu s’expriment beaucoup plus facilement qu’on aurait pu penser !

Meu) 42 est la réponse…

D’après la formule précédente, pour trouver les diviseurs de GaBuZoMeu…GaBuZoMeu, il suffit de trouver les diviseurs de $2^{8n} - 1$ . Il se trouve que ce dernier est un nombre de Mersenne c’est-à-dire un nombre de la forme $2^k - 1$ mais ce n’est pas cela que nous allons utiliser pour le moment.

D’après le théorème d’Euler, on sait que pour tout nombre impair $m$ , comme 2 est premier avec $m^2$ alors $2^{\varphi(m^2)} \equiv 1 \mod[m^2]$ où $\varphi$ est la fonction indicatrice d’Euler. En prenant la puissance 8 des deux côtés de cette relation, on obtient

$2^{8\varphi(m^2)} \equiv 1 \mod[m^2]$

Cela veut donc dire que $m^2$ divise toujours $2^{8 \varphi(m^2)}-1$ . Pour trouver des contre-exemples, il suffit donc de choisir un nombre impair $m$ et de poser $n=\varphi(m^2)$ ; le nombre $m^2$ divisera alors $2^{8n}-1$ .

Par exemple, si on prend $m=7$ , cela donne $n=\varphi(7^2) = 42$ . D’après ce qu’on vient de voir, le nombre $2^{8 \times 42}-1$ est divisible par $7^2$ (vous ne me croyez pas ?) donc notre conjecture est fausse car le nombre GaBuZoMeu…GaBuZoMeu (42 fois) est divisible par $7^2$ . Sur le même principe, on peut même construire une infinité de contre-exemples en prenant $n=\varphi(m^2)$ où $m$ est presque n’importe quel nombre impair !

Je dis « presque » car on ne pouvait pas prendre $m=5$ (ce qui donnerait $n = \varphi(5^2)= 20$ ) car, bien que $2^{8 \times 20}-1$ est divisible par $25 = 5^2$ , il ne faut pas oublier qu’il y avait un facteur 5 au dénominateur du nombre $\dfrac{3^2 (2^{8n}-1)}{5 \times 17}$ , nombre qui ne serait donc pas forcément divisible par 25. De même, pour $m=17$ , le nombre $n= \varphi(17^2) = 272$ n’est pas forcément un contre-exemple car il n’est pas nécessairement divisible par $17^2$ . Enfin, pour $m=3$ (et donc $n=\varphi(3^2) = 6$ ), la seule chose qu’on pourrait dire du nombre GaBuZoMeu…GaBuZoMeu (6 fois), c’est qu’il est divisible par $3^2$ , ce qui était autorisé dans notre conjecture. Enfin, prendre $m=1$ n’a aucun intérêt car cela voudrait juste dire que le nombre est divisible par $1^2$ (voilà enfin la fameuse remarque à la con que l’on retrouve dans chaque article de ce blog).

Ainsi, $n=42 = \varphi(7^2)$ était donc le plus petit contre-exemple possible avec cette méthode et voici la liste des premiers contre-exemples obtenus similairement (c’est-à-dire en prenant $n = \varphi(m^2)$ pour $m$ impair différent de 1, 3, 5 et 17):

$n = 42, 54, 110, 156, 120, 342, 252, 506, 500, 486, 812, 930, 660, 840, 1332, \\ 936, 1640, 1806, 1080, 2162, 2058, 1632, 2756, 2200, 2052, 3422, 3660, 2268, 3120, \\ 4422, 3036, 4970, 5256, 3000, 4620, 6162, 4374, 6806, 5440, 4872, 7832, 6552, 5580, \\ 6840, 9312, 5940,...$

Vous remarquez que tous ces contre-exemples sont pairs. Sans rentrer dans les détails, cela vient du fait (pas difficile à prouver) que $\varphi(a)$ est un nombre pair si $a>1$ est un nombre impair. Une question légitime que l’on pourrait alors se poser est: existe-t-il des contre-exemples avec $n$ impair ? Pour le savoir, il va falloir étudier les choses d’un peu plus près…

BuGa) À la recherche d’autres contre-exemples

Nous allons affiner notre recherche de contre-exemples grâce à une propriété donnant une condition nécessaire pour qu’un nombre de Mersenne d’exposant un nombre premier possède un facteur carré. La voici (et vous pourrez en trouver une démonstration en fin d’article):

Si un nombre de Mersenne $2^q - 1$ (avec $q$ premier) est divisible par $p^2$ où $p$ est un nombre premier, alors $p$ est un nombre premier de Wieferich.

Là, c’est le moment où tout le monde se demande ce que peut bien être un nombre premier de Wieferich. Un nombre premier de Wieferich est un nombre premier $p$ tel que $p^2$ divise le nombre de Mersenne $2^{p-1}-1$ . Par exemple, le nombre premier $p=1093$ est un nombre de Wieferich car son carré divise le nombre $2^{1093-1}-1 = 2^{1092}-1$ (vous ne me croyez toujours pas ?).

Des nombres premiers de Wieferich, il n’y en a pas beaucoup. A vrai dire, on n’en connaît que deux à l’heure actuelle : 1093 et 3511. Cependant, vous allez voir que cela nous sera largement suffisant !

Revenons au nombre GaBuZoMeu…GaBuZoMeu ( $n$ fois) dont a vu qu’il était égal à $\dfrac{3^2 \left(2^{8n}-1\right)}{5\times 17}$ . Pour montrer qu’il possède un facteur carré, il suffirait de faire apparaître $2^{1092}-1$ dans cette expression, de sorte que $1093^2$ diviserait ce nombre.

Pour faire cela, commençons par remarquer qu’on a la factorisation suivante (merci aux identités remarquables !):

$X^{8n} - 1 = (X^{4n})^2 - 1^2 = (X^{4n} -1) (X^{4n}+1)$

Or, $X^{4n}-1 = (X^{2n})^2 - 1^2 = (X^{2n} -1) (X^{2n}+1)$ donc

$X^{8n}-1 = (X^{2n} -1) (X^{2n}+1)(X^{4n}+1)$

Comme $(X^{2n} -1) = (X^n - 1) (X^n +1)$ , on a donc

$X^{8n}-1 = (X^n - 1) (X^n +1)(X^{2n}+1)(X^{4n}+1)$

Nous pouvons donc à présent transformer l’expression de $N$ = GaBuZoMeu…GaBuZoMeu en

$N = \dfrac{3^2 \left(2^{8n}-1\right)}{5\times 17} = \dfrac{3^2 (2^n - 1) (2^n +1)(2^{2n}+1)(2^{4n}+1)}{5\times 17}$

Nous voyons donc qu’en prenant $n = 1092$ , le nombre GaBuZoMeu…GaBuZoMeu (où GaBuZoMeu est répété 1092 fois) s’écrira

$N = \dfrac{3^2 (2^{1092} - 1) (2^{1092} +1)(2^{2184}+1)(2^{4368}+1)}{5\times 17}$

et il sera bien divisible par $1093^2$ car $1093$ est un nombre premier de Wieferich c’est-à-dire que $1093^2$ divise $2^{1092}-1$ . Nous voilà donc avec un autre contre-exemple à notre conjecture qui n’était pas dans notre liste !

Cependant, 1092 n’est pas un contre-exemple impair donc nous n’allons pas nous arrêter là dans notre recherche. On sait que $1093^2$ divise $2^{1092}-1$ , mais en fait il divise des nombres de Mersenne plus petits encore. Un petit algorithme permet de voir que $1093^2$ divise aussi $2^{728}-1$ et même $2^{364} -1$ . Ainsi, de la même façon que précédemment on voit qu’en prenant $n=728$ ou $n=364$ on obtient deux nouveaux contre-exemples à notre conjecture qui n’étaient pas dans notre liste.

Mais on peut encore faire mieux ! Il se trouve que le nombre $728$ est un multiple de 8 car $728 = 8 \times 91$ . En reprenant la première formule que nous avions vue, à savoir $N= \dfrac{3^2 \left(2^{8n}-1\right)}{5\times 17}$ , pour $n=91$ , on obtient:

$N= \dfrac{3^2 \left(2^{8\times 91}-1\right)}{5\times 17} = \dfrac{3^2 \left(2^{728}-1\right)}{5\times 17}$

ce qui prouve que le nombre GaBuZoMeu…GaBuZoMeu où GaBuZoMeu est répété 91 fois est divisible par $1093^2$ et n’est donc pas sans facteur carré ! On peut même le vérifier « directement » car ce nombre à 219 chiffres (!) est égal à

$149506621343376220426717526940245004530365795333318\ \\ 81013029774928096614396029874411266391346445335278\ \\ 08122399381444468776653510105465030501684645752728\ \\ 38323281630381313790853442080521484907833820669507\ \\ 266526533960538907$

et sa décomposition en produit de facteurs premiers est

$3^3 \times 29 \times 43 \times 53 \times 113 \times 127 \times 157 \times 911 \times 1\,0 93^2 \times 1 \, 613 \times 2 \, 731 \times 4 \, 733 \times 8 \, 191 \times 224 \, 771 \times 858 \, 001 \times 1 \, 210 \, 483 \times 15 \, 790 \, 321 \times 112 \, 901 \, 153 \times 308 \, 761 \, 441 \times 23 \, 140 \, 471 \, 537 \times 25 \, 829 \, 691 \, 707 \times 593 \, 914 \, 915 \, 675 \, 537 \times 8 \, 861 \, 085 \, 190 \, 774 \, 909 \times 556 \, 338 \, 525 \, 912 \, 325 \, 157 \times \\ 88 \, 969 \, 9 72 \, 427 \, 0 95 \, 486 \, 8 38 \, 263 \, 4 04 \, 334 \, 1 55 \backslash \\ \, 574 \, 0 24 \, 974 \, 1 98 \, 424 \, 7 57 \, 8510 \, 445 \, 178 \, 451 \, 442 \, 481 \, 793$

Vous voyez donc bien qu’il y a un facteur carré ! Cela dit, il restera une question en terminant cet article: $n=91$ est-il le plus petit contre-exemple impair à cette conjecture ?

Notes:

Les calculs de décomposition en produit de facteurs premiers ont été effectués grâce à ce site (qui utilise la méthode de factorisation par les courbes elliptiques… fallait bien ça pour factoriser des nombres de 219 chiffres !)
Voici une démonstration de la propriété disant que si un nombre de Mersenne d’exposant premier est divisible par un facteur carré alors il est divisible par un nombre premier de Wieferich.

14 commentaires pour GaBuZoMeu…GaBuZoMeu

Anonyme dit :

24 septembre 2017 à 14 h 02 min

Bonjour,
Le dernier nombre affiché, pour n=91, est faux. Son expression est correcte, mais pas son écriture décimale. Il manque un 1 au début.
(Vous ne me croyez pas 😉 ? http://www.wolframalpha.com/input/?i=3%5E2*(2%5E728-1)%2F(5*17) )

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  24 septembre 2017 à 14 h 37 min
  
  En effet, il manque un 1 au début ! D’ailleurs, si vous comptez, vous voyez qu’il n’y a que 218 chiffres alors que j’affirme que c’est un nombre à 219 chiffres… Je vais réparer cette coquille de ce pas !
  
  J’aimeJ’aime
  
  Réponse
Anonyme dit :

24 septembre 2017 à 14 h 09 min

Quant à la conjecture, le plus petit contre-exemple impair n’est pas n=91, mais n=21.
Pour n=21, on trouve que 7² divise le nombre obtenu. Et c’est bien le plus petit contre-exemple impair.
http://www.wolframalpha.com/input/?i=Factor%5B3%5E2*(2%5E(8*21)-1)%2F(5*17)%5D

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  24 septembre 2017 à 14 h 43 min
  
  Tout à fait, n=21 semble bien être le plus petit contre-exemple impair ! Je vous pose alors une autre question: y a-t-il d’autres contre-exemples impairs entre 21 et 91 ? et si oui lesquels ? 🙂
  
  (Il y en a au moins 3 autres 😉 )
  
  J’aimeJ’aime
  
  Réponse
  - Anonyme dit :
    
    25 septembre 2017 à 1 h 32 min
    
    J’en trouve même exactement quatre autres, entre n=21 et n=91 :
    * n=25, qui est divisible par 5²,
    * n=39, qui est divisible par 13²,
    * n=55, qui est divisible par 11²,
    * n=75, qui est divisible par 5².
    
    J’aimeJ’aime
    
    Réponse
    - blogdemaths dit :
      
      25 septembre 2017 à 11 h 33 min
      
      Effectivement, n=25, 39, 55 et 75 marchent ! 🙂
      
      Il y en a même un autre: pour n = 63, le nombre est divisible par 7².
      
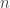      Ce qui m’amène à une dernière conjecture (à laquelle j’avoue ne pas encore avoir réfléchi): est-ce que pour tout nombre premier impair $p$ , il existe un entier $n$ impair tel que le nombre obtenu pour ce 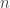$n$ soit divisible par $p^2$ ?
      
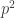      J’aimeJ’aime
Ping : Les shadoks comptent aussi – Pierre Carrée
Ping : Una conjetura sobre ciertos números en el ‘sistema Shadok’ - Cuaderno de Cultura Científica
ALLAIN François dit :

29 septembre 2017 à 12 h 29 min

Bonjour,
Je suis incapable d’apprécier la démonstration faite mais je trouve sympa d’utiliser les Shadocks pour cette démonstration.

Par contre, je suis surpris : vous parlez d’un système en base 4 alors qu’il me semble être en base 3 (le zéro ne compte pas).

Si je tiens compte du zéro, notre système « décimal » serait en base 11 !

Pouvez-vous m’aider à comprendre cette apparente contradiction ?

Merci d’avance.

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  29 septembre 2017 à 16 h 28 min
  
  Bonjour,
  
  On parle d’un système en base 4, car on utilise quatre chiffres pour pouvoir écrire tous les autres. Ces chiffres sont 0, 1, 2 et 3. Le zéro compte bel et bien comme un chiffre !
  
  Dans le système décimal (base 10), on utilise dix chiffres pour écrire tous les autres. Ces dix chiffres, vous les connaissez, ce sont 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. Là encore, zéro compte bien comme un chiffre.
  
  J’espère avoir répondu à votre interrogation !
  
  J’aimeJ’aime
  
  Réponse
  - ALLAIN dit :
    
    29 septembre 2017 à 16 h 38 min
    
    Merci de votre réponse.
    
    Ma question méritait un zéro pointé !
    
    Merci encore.
    
    J’aimeJ’aime
    
    Réponse
Anonyme dit :

11 janvier 2019 à 16 h 12 min

Mais c’est génial cette page ! Personne ne le dit.

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  22 janvier 2019 à 19 h 53 min
  
  Merci de la dire alors… 😀
  
  J’aimeJ’aime
  
  Réponse
Anonyme dit :

31 mars 2024 à 14 h 27 min

Je trouve cette page intéressante et les choses sont bien expliquées.

J’aimeJ’aime

Réponse

Laisser un commentaire Annuler la réponse.

Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur la façon dont les données de vos commentaires sont traitées.