La semaine dernière, le jeu de hasard Euro Millions fêtait ses 10 ans et nombreux furent les articles dans la presse ou à la télévision autour de ce jeu. J’ai pu constaté un certain nombre de bêtises relayées dans les médias et même sur Internet où, nombreux sont les sites qui prétendent savoir quels numéros jouer (ou ne pas jouer) en se basant sur les statistiques des derniers tirages (!). Pourquoi ne pas faire un article sur l’Euro Millions dans lequel on examinerait mathématiquement toutes ces affirmations (ou supersitions) ?
Les deux plus grandes idées reçues que j’ai vu étaient:
- a) Il y a des numéros qui ont plus de chances de sortir que d’autres;
- b) Si un numéro n’est pas sorti depuis longtemps, alors il a plus de chances de sortir au prochain tirage.
Nous allons dans cet article essayer d’analyser ces énoncés, ce qui nous donnera l’occasion de faire un peu de dénombrement, un peu de statistiques inférentielles et un peu de chaînes de Markov. Comme il est bien entendu impossible d’expliquer en un seul article toute la théorie autour de ces concepts, j’ai essayé de résumer à chaque fois les résultats mathématiques obtenus.
0) Le cadre de l’Euro Millions
Le jeu de l’Euro Million consiste à choisir une combinaison de 5 nombres entre 1 et 50 ainsi qu’une combinaison de 2 nombres « étoiles » choisis entre 1 et 11 (voir la page Wikipédia à ce sujet pour plus de précisions). Pour simplifier l’étude que nous allons faire, nous allons laisser de côtés ces numéros étoilés et simplement nous intéresser aux 5 numéros choisis parmi 50.
Information importante: il y a eu (au moment où j’ai commencé à écrire cet article) environ 668 tirages depuis le début de l’Euro Millions en 2004. Je tire cette information des nombreux sites non officiels qui répertorient les statistiques de l’Euro Millions car la Française des Jeux ne publie mystérieusement pas cette information (voir explication probable plus loin dans cet article). Nous pouvons néanmoins faire confiance à ces sites pour cette valeur de 668 tirages car d’une part cette valeur concorde sur tous les sites et d’autre part, j’ai trouvé la même valeur le site officiel de la loterie anglaise.
1) Quelle la probabilité théorique qu’un numéro donné soit tiré ?
Commençons par calculer la probabilité qu’un numéro donné soit choisi lors d’un tirage et, pour cela, on fait l’hypothèse que le tirage est effectué de façon équiprobable. Contrairement, à ce qu’on pourrait croire à première vue, cette probabilité n’est pas de 1/50 mais est plus grande. D’un point de vue heuristique, cela peut se comprendre car chaque tirage consiste à tirer 5 numéros de suite (sans remise) donc si un numéro n’a pas été tiré la première fois, il peut être tiré la deuxième, troisième, quatrième ou cinquième fois. Plus rigoureusement, chaque tirage est une partie à 5 éléments dans un ensemble à 50 éléments. Il y a donc grilles possibles !
Attention, cela peut paraître peu, mais n’oublions pas qu’ici nous ne nous intéressons pas aux deux numéros étoilés supplémentaires… Si on les prend en compte, il y a alors grilles possibles ce qui donne une probabilité de
de gagner le Jackpot. Ca fait réfléchir avant de jouer…
Revenons à nos numéros. Quelle est la probabilité qu’un numéro donné sorte ? Pour le savoir, il faut dénombrer les grilles possibles auxquelles peut appartenir ce numéro. Pour fixer les idées, prenons le numéro 50. Il peut par exemple appartenir à la grille 4-12-23-26-50 ou bien il peut aussi appartenir à la grille 6-9-12-34-50. En fait, il y a autant de grilles auxquelles il appartient que de façons de choisir 4 numéros parmi les 49 qui restent, c’est-à-dire . On en déduit que la probabilité
que le numéro 50 (ou n’importe quel numéro, le raisonnement est le même) soit tiré est :
Chaque numéro a donc une chance sur 10 de sortir ! La loi des grands nombres (qui est un vrai théorème mathématique !) nous dit alors que, plus il y aura de tirages de l’Euro Millions, plus la fréquence de sortie de chaque numéro se rapprochera de 0,1 (10%). On pourra donc faire toutes les statistiques que l’on veut, la tendance pour chaque numéro sera d’avoir une fréquence qui se rapproche de 0,1. Cependant, il peut y avoir quelques fluctuations…
2) Existe-t-il des numéros qui ont plus de chances de sortir quand même ?
Nous avons vu que chaque numéro a la même probabilité théorique de sortir égale à 0,1. Cependant, certains sites affirment en se basant sur l’observation que, puisque certains numéros sont sortis beaucoup de fois jusque-là, c’est qu’ils ont plus de chances d’apparaître en général. Après tout, peut-être que le tirage de l’Euro Millions est biaisé et qu’effectivement certains numéros sont favorisés par rapport à d’autres ? Par exemple, le numéro le plus sorti est le 50 et il est sorti 87 fois sur les 668 tirages effectués depuis les débuts de l’Euro Millions, ce qui représente une fréquence d’environ . Nous allons confronter cette information à deux hypothèses possibles. Si on note
la probabilité que 50 soit tiré:
- 1ère hypothèse:
- 2ème hypothèse:
(comme certains sites l’affirment).
Nous allons essayer de voir quelle hypothèse on peut garder (avec un certain risque d’erreur) de la façon suivante: en supposant que la 1ère hypothèse soit vraie, nous allons émettre une règle de décision, c’est-à-dire une règle qui permettra, à partir d’un échantillon observé, de dire si oui ou non on garde cette hypothèse. Si on ne garde pas cette 1ère hypothèse, on considérera que c’est la 2ème hypothèse qui est correcte (autrement dit que 50 a bien plus de chances de sortir). Cette démarche s’appelle un test d’hypothèse.
Pour émettre cette règle de décision, il faut au préalable un peu de calculs. Si on effectue tirages de l’Euro Millions et si
est la variable aléatoire qui compte le nombre de fois où 50 est sorti, alors
suit une loi binomiale
(les tirages sont supposés indépendants). Comme le nombre de tirages
est suffisamment grand, on peut affirmer (via le théorème de Moivre-Laplace) que
suit approximativement la loi normale
et donc la fréquence
d’apparition de 50 suit approximativement la loi normale
. Dans le cas où on suppose que la 1ère hypothèse est vraie, alors
et puisqu’il y a eu
tirages, on peut donc considérer que
suit la loi
:

Dans l’hypothèse où p=0,1 la fréquence d’apparition du numéro 50 suit cette distribution de probabilité. L’axe des abscisses représente les fréquences possibles observée et on voit que sous l’hypothèse où p=0,1, la fréquence d’apparition la plus probable est 0,1. On voit déjà que les fréquences balayées vont de 0,06 à 0,14 environ.
On souhaite savoir à partir de quelle fréquence observée on pourra considérer que notre hypothèse n’est plus valable, avec un risque d’erreur disons de 0,1% (1 pour mille). Mathématiquement, cela revient à chercher le nombre tel que
(voir schéma ci-dessous):

On cherche le nombre x de sorte que la probabilité que la fréquence observée se situe dans les abscisses de la zone rouge soit de 1 pour mille. L’aire colorée en rouge s’appelle la zone critique et est égale à P(F>0,1+x).
En introduisant la variable dont on sait qu’elle suit la loi normale centrée réduite, on a alors:
A l’aide d’une table de la loi normale centrée réduite, on trouve qu’il faut c’est-à-dire
. Ainsi,
. On émet donc la règle de décision suivante:
- Si à l’Euro Millions, la fréquence observée d’un nombre est inférieure à 13,6% alors on peut considérer que sa probabilité théorique d’apparition est bien de 0,1 (avec une probabilité de se tromper de 1 pour mille).
- Sinon, on peut considérer que sa probabilité théorique d’apparition est supérieure strictement à 0,1.
Comme la fréquence du numéro 50 est , elle entre dans le premier cas de figure: on peut donc penser qu’il n’y a très probablement aucune raison à considérer que les tirages de l’Euro Millions sont biaisés et que, même si la fréquence de sortie du numéro 50 est supérieure à sa fréquence théorique de 0,1, cette différence observée est très probablement due aux fluctuations d’échantillonnage et n’est pas significative.

Comme la fréquence observée (13%) n’est pas dans la zone critique, on garde l’hypothèse p=0,1 et on rejette l’hypothèse p>0,1
Conclusion (pour ceux qui n’auraient rien compris à tous ces raisonnement imbitables, je l’admets…): Notre test d’hypothèse montre qu’il n’y a (très probablement) pas de raison de penser que certains numéros sortent plus souvent.
(Remarque: on peut tout à fait discuter le choix du seuil de risque à 0,1%. Pour un choix de 5% ou de 1%, la fréquence 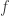 serait dans la zone critique et l’hypothèse
serait dans la zone critique et l’hypothèse  serait alors à rejeter. Pour préciser les choses dans le cas du seuil de risque que nous avons choisi (0,1%) et pour lequel nous avons accepté l’hypothèse
serait alors à rejeter. Pour préciser les choses dans le cas du seuil de risque que nous avons choisi (0,1%) et pour lequel nous avons accepté l’hypothèse  , on pourrait calculer la probabilité d’accepter cette hypothèse sachant qu’elle est fausse. Cette probabilité s’appelle le risque de seconde espèce; nous n’allons pas la calculer ici (elle est à vue de nez un peu plus grande que 50%), mais c’est une probabilité qui dépend inversement de notre seuil de risque et qui sera augmentée d’autant plus que notre seuil est petit. Si on avait pris un seuil de risque plus grand, cette probabilité aurait été plus petite.)
, on pourrait calculer la probabilité d’accepter cette hypothèse sachant qu’elle est fausse. Cette probabilité s’appelle le risque de seconde espèce; nous n’allons pas la calculer ici (elle est à vue de nez un peu plus grande que 50%), mais c’est une probabilité qui dépend inversement de notre seuil de risque et qui sera augmentée d’autant plus que notre seuil est petit. Si on avait pris un seuil de risque plus grand, cette probabilité aurait été plus petite.)
Notons qu’on a pu faire ce test car l’échantillon de numéros sortis est suffisamment important (notre calcul est basé sur un nombre de tirages suffisamment grand). Pourtant, les statistiques officielles de la Française des Jeux sont quant à elles beaucoup moins nombreuses et ne remontent qu’à il y a 3 ans (ce qui correspond au moment où les numéros étoilés sont passés de « 1-9 » à « 1-11 »,ce qui, d’ailleurs, a diminué la probabilité de gain…). Cela est sans doute volontaire, car plus l’échantillon est faible, moins il y de chance que les fréquences d’apparition soient proches de leurs probabilités réelles et plus on peut faire croire aux gens que certains numéros ont plus de chances de sortir que d’autres. Par exemple, depuis 3 ans le 28 est sorti 14,2% des tirages (ce qui est assez élevé et non significatif car le nombre de tirages est petit) alors que depuis 2004, il n’est sorti que 10,1% des fois. Le but est peut-être d’induire le parieur en erreur… du moins, je ne vois aucune autre explication au fait de ne pas mettre toutes les statistiques depuis la création du jeu.
3) Si un numéro n’est pas sorti depuis longtemps, a-t-il plus de chances de sortir au prochain tirage ?
La réponse est évidemment non et penser (ou, pire, écrire…) le contraire est l’erreur de raisonnement connue sous le nom d’Erreur du parieur. Les tirages sont indépendants et tout recommence à zéro à chaque fois ! C’est comme à Pile ou Face: si vous venez d’obtenir 10 fois Pile de suite, alors est-ce pour autant que Face aura plus de chances d’apparaître lors du 11ème lancer ? Eh bien non. C’est pareil pour l’Euro Millions: ce n’est pas parce qu’un nombre n’est pas sorti depuis longtemps qu’il a plus de chances de sortir au prochain tirage. A l’inverse, j’ai vu des sites affirmer que, puisqu’un numéro vient de sortir depuis peu, il ne faut pas le jouer car il est censé ne pas réapparaître avant un bout de temps… ce qui est également absurde !

Voici le genre de conseils donnés sur certains sites (que je préfère ne pas nommer…) basés sur les statistiques de tous les tirages de l’Euro Millions. Vous apprécierez le vocabulaire numérologiste. Du grand n’importe quoi.
En revanche, ce qui est vrai, c’est qu’en moyenne sur un grand nombre de tirages, chaque numéro est retiré toutes les 10 fois. Pour prouver cela, nous allons calculer ce qu’on appelle le temps moyen de réapparition c’est-à-dire le nombre moyen de tirages qui s’écoulent pour qu’un numéro soit tiré à nouveau.
Si on répète les tirages de l’Euro Millions, nous avons dit que ce qui s’est passé au tirage précédent n’influence pas ce qui va se passer au tirage présent. Il s’agit d’un cas très très particulier de chaîne de Markov (rassurez-vous, vous n’avez rien besoin de connaître de la théorie des chaînes de Markov pour comprendre la suite). On peut représenter cette chaîne de Markov à l’aide d’un graphe (par exemple dans le cas de la boule numéro 50 histoire de fixer les idées, mais le principe est le même pour n’importe quel numéro):

Le nœud « 50 » correspond à l’événement: « Le numéro 50 est sorti lors du tirage ». Le nœud « non 50 » signifie: « 50 n’est pas sorti lors du tirage ». La flèche partant de « non 50 » et allant à « 50 » correspond à la probabilité de tirer 50 sachant qu’au tirage précédent on n’a pas tiré 50. Comme les événements sont indépendants, cette probabilité est bien 0,1. Idem pour les autres flèches.
On note le temps de retour en 50, c’est-à-dire le nombre de tirages qui sont effectués avant que le nombre 50 ne soit retiré de nouveau. Calculons par exemple la probabilité de l’événement « le numéro 50 vient d’être tiré et il n’est retiré que 4 tirages après »:
Dans le cas général, nous voyons (sur le même principe) que la probabilité de ne retirer 50 qu’après tirages est
. Pour calculer l’espérance
de cette variable (qui est par définition le temps moyen de réapparition), il faut pondérer chaque temps de réapparition
par sa probabilité
. Ainsi:
On peut montrer que le membre de droite converge vers 10 (par exemple en utilisant la formule ). Le temps moyen pour un numéro d’être retiré est donc de 10 tirages.
Conclusion: Bien que sur un tirage tout est possible et que rien ne dépend de ce qui s’est passé lors des parties précédentes, sur le long terme, chaque numéro possède un temps moyen de réapparition qui est de dix tirages. Cependant, cela ne veut absolument pas dire que si un numéro n’est pas sorti 9 fois alors il sortira la 10ème fois mais simplement que sur un grand nombre de tirages, une tendance de réapparition moyenne tous les 10 tirages se dégagera.
C’est un résultat difficile à concevoir intuitivement et cela sème sans doute le trouble chez le parieur. Lorsqu’on fait un grand nombre de tirages, on se rendra compte que chaque numéro est sorti en moyenne tous les 10 tirages, mais il se pourra par exemple qu’il se soit produit de nombreux tirages avant qu’un numéro donné ne ressorte (c’est le cas par exemple du numéro 48 qui n’est pas sorti pendant 82 tirages de suite !).
4) Comment alors réellement optimiser ses chances à l’Euro Millions ?
Pour cette partie, je vais suivre les analyses données par Jean-Paul Delahaye dans cet article dont je vais tenter de retranscrire quelques idées du mieux possible (en espérant qu’il ne m’en veuille pas !).
Puisqu’il n’y a rien que l’on puisse faire pour augmenter les probabilités qu’une grille sorte, autant augmenter l’argent ramassé dans le cas où on gagnerait. Il se trouve que, dans les règles de l’Euro Millions, si plusieurs personnes jouent et gagnent avec la même combinaison, alors les gains sont partagés. Puisque toutes les combinaisons sont équiprobables, le parieur a donc tout intérêt à choisir une combinaison qui est peu jouée par les autres joueurs. Encore faudrait-il savoir quels sont les numéros joués par les autres joueurs en général… Et ça, c’est pas facile à savoir car il se trouve que la Française des Jeux refuse volontairement de donner les statistiques sur les numéros et les grilles effectivement jouées par les parieurs. Comme le note J-P Delahaye à juste titre: « C’est assez étrange et malsain, puisqu’en se comportant ainsi, la Française des Jeux encourage les comportements superstitieux et décourage les comportements rationnels ».
Cela n’a pourtant pas empêché des statisticiens de retrouver les fréquences des numéros joués par les Français dans le cas du Loto (autre jeu de la Française des Jeux) en se basant sur l’unique information qu’on ne peut pas ne pas publier: les combinaisons gagnantes et le nombre de gagnants pour chacune ! On s’est donc rendu compte que les numéros les plus joués étaient le 7, le 9 et le 13. Si vous voulez augmenter vos gains à l’Euro Millions (dans le cas où votre grille est tirée), choisissez les numéros les moins joués par les Français: 32, 38, 39, 40 et 41.
Bon, je sais, vous allez me dire que maintenant que la France entière sait quelle combinaison jouer (car c’est bien connu, ce blog reçoit des millions de visites chaque jour), cela va diminuer le gain qu’on pourrait en tirer… Mais comme le dit J-P Delahaye: « Le fait que ces numéros les moins joués aient été publiés peut avoir une influence sur les prochains tirages, mais elle sera probablement assez faible et donc une grille utilisant des numéros parmi les moins joués dans le passé a toutes les chances d’être une grille peu jouée dans le futur. »
5) Mais quand même, n’y a-t-il pas un moyen sûr à 100% de gagner à l’Euro Millions ?
La seule stratégie gagnante à l’Euro Millions, avec une probabilité de 1, c’est de s’appeler la Française des Jeux (ou l’État Français). La raison principale en est que le taux de redistribution de l’Euro Millions est ridiculement bas: 50% uniquement. Pour une grille validée à 2 euros, seul 1 euro sera reversé dans la cagnotte des gains, le reste allant bien gentiment dans la poche de la Française des Jeux. Réjouissons-nous quand même: cela permet à l’État Français de collecter un peu (beaucoup d’argent) dans une sorte d’impôt joyeux, où les joueurs payent dans l’espoir d’obtenir un gain qui changerait leur vie. Alors certes, personne n’est obligé de jouer à ce jeu, mais quand on sait que ce sont les employés et les ouvriers qui jouent le plus (et cela se comprend bien que ce soit les classes les plus pauvres qui soient les plus tentées par le rêve d’une vie meilleure, rêve vendu à longueurs de publicités), on peut penser que ce jeu fait son beurre sur la misère des gens. Pendant ce temps, cette entreprise a doublé son chiffre d’affaires depuis 2000, culminant à plus de 12 milliards d’Euros en 2013.
Bref, si vous voulez gagner à l’Euro Millions, n’y jouez pas.



Article très intéressant et qui me laisse toujours perplexe avec les stats inférentielles.
Peut-être que je vais adapter la partie test d’hypothèses pour mes bts.
Le problème étant le choix du seuil: plus le seuil est petit plus la zone d’acceptation est grande.
Du coup prendre un seuil à 0,1% est-il judicieux ?
Et prendre un seuil de 5% plus habituel fournit une conclusion contraire à ce que l’on veut prouver !
J’aimeJ’aime
C’est une question très intéressante à laquelle j’ai pas mal réfléchi en écrivant cet article.
Comme je l’ai dit dans l’article, le choix du seuil à 0,1% est parfaitement discutable.
J’ai essayé d’organiser ma réponse en plusieurs remarques:
1) Effectivement, plus le seuil est petit et plus la zone d’acceptation est large… cependant, comme on le voit sur la distribution probabiliste des fréquences (voir schéma dans l’article de la distribution normale), dans le cas où l’hypothèse nulle (p=0,1) est vraie alors quasiment 100% des fréquences seront comprises entre 6% et 14%. On sent déjà qu’une fréquence observée de 20% (ou même plus) pourrait significativement montrer que la boule 50 a plus de chances d’être tirée.
(Rappelons au passage que si la fréquence observée est dans la zone acceptable, cela ne montre pas que l’hypothèse nulle est vraie, mais simplement que cet échantillon n’a pas réussi à faire rejeter le test…)
2) Le numéro 50 est la boule sortie le plus souvent, mais la plupart des autres boules passeraient le test pour un seuil de 5%. Il se trouve qu’on a étudié ici une fréquence maximale dont on peut penser a priori qu’elle est potentiellement due à une grande fluctuation, ce qui peut inciter à prendre un seuil de risque plus petit.(même si dans un test d’hypothèse on choisit le seuil avant l’observation !)
3) Rappelons d’ailleurs la définition du seuil de risque: c’est la probabilité que l’hypothèse nulle soit rejetée sachant qu’elle est vraie.
Si on choisit un seuil de risque de 5%, on aura donc 5 chances sur 100 que notre fréquence observée nous fasse rejeter l’hypothèse nulle si jamais celle-ci était vraie dans l’absolue. On peut donc penser que, si l’hypothèse nulle est vraie, alors:
(si on considère que toutes les boules sont identiques)
– parmi les 50 boules, il y en aura environ 2 ou 3 (cad environ 5%) qui nous feraient rejeter ce test ;
ou bien (si on ne s’intéresse qu’à la boule 50 spécifiquement),
– si on refaisait 100 fois les 668 tirages, dans 5 cas environ nous aurions une fréquence de 50 dans la zone critique.
En bref, si on utilisait le seuil de 5% et que la fréquence nous faisait échouer le test, on pourrait dire qu’il y avait a priori 5 chances sur 100 que la fréquence de 50 fasse échouer le test sachant que l’hypothèse nulle est vraie. Ici, nous avons fait le test de façon à ce qu’il y ait une chance sur 1000 que la fréquence observée nous fasse échouer le test sachant que l’hypothèse nulle est vraie.
4) Il faut comprendre que le choix du seuil est à la base arbitraire et que le choix habituel de 5% n’a pas plus de légitimité qu’un autre pourcentage. Cela dépend uniquement du niveau de risque qu’on souhaite à la base c’est-à-dire de la marge d’erreur qu’on décide à priori de se donner (probabilité de rejeter l’hypothèse nulle sachant qu’elle est vraie). Un seuil très petit (comme 1 pour mille) correspond à un niveau de significativité très haut.
Mais alors dans ce cas, vous allez me dire : pourquoi ne pas toujours prendre un seuil le plus petit possible alors ?
Il faut aller chercher dans une notion qui n’est pas enseignée en BTS je crois, qui est celle de risque de seconde espèce. Comme dit dans la remarque en petits caractères dans l’article, le risque de seconde espèce est la probabilité d’accepter l’hypothèse nulle sachant qu’elle est fausse. Et, il se trouve (on va l’admettre) que cette probabilité est d’autant plus grande que le seuil de risque est petit et que pour un seuil de risque de 1/1000, cette probabilité est plus grande que 50% d’après les estimations que j’ai faites (ce qui est beaucoup). Pour diminuer cette probabilité, on peut soit prendre le seuil plus grand, soit augmenter l’échantillon…
Mais encore une fois, un test d’hypothèse ne donne au final une réponse qu’avec une certaine probabilité. Il n’y a pas de certitude… C’est donc pour cela qu’on émet une règle de décision.
Je finirai en disant que la seule façon de préciser un test est d’augmenter la taille de l’échantillon. Si on attend une centaine de tirages de plus de l’Euro Millions, on pourra refaire le test et voir à ce moment-là ce qu’il en est !
J’aimeJ’aime
et comment calculer nos chances si on paye 45€ pour 6 n° + 3 étoiles = 1/7768787… mais comment le calculer ?
EXCEL : =COMBIN(50;5)*COMBIN(12;2) = 139838160
mais pour 6+3 ?
J’aimeJ’aime
Le plus simple, puisqu’ une combinaison coute 2.5 eur, alors pour 45 eur il y a (45/2.5) = 18x plus de chance donc 139838160/18 = 7768786.667. Si non calculer avec les factorielles.
J’aimeJ’aime
Bonjour, je rejoins la conclusion de l’auteur. Faute d’euros millions, les gouvernants ne pourraient pas agir comme ils le font (Analyse faite sur le comportement humain). L’espoir est la capsule du désespoir. Ne jouez pas vous serez les gagnants, c’est un impôt supplémentaire et de surcroît divisé 2,50 euros et vous découvrirez la supercherie des mises epsilons mises en jeu par rapport au nombre de joueurs.
Sur l’exposé je suis en accord logique de la démonstration bien présentée et exposée. J’ai pour ma part, fait quelques expériences de probabilités sur l’euros millions et je conclus : La théorie des chiffres et leur répétitivité de sortie apporte, dans le sens tout aussi logique que l’auteur, un autre constat relatif entre une moyenne logique de la sommes d’une combinaison avec la théorie en pourcentage du nombre de fois que sort un numéro. Tout ceci apporte en quel que sorte une moyenne presque constante. « Exemple » la moyenne de la somme d’une combinaison est 20. Nous pouvons constater régulièrement cette moyenne, effectivement composé de tous les nombres mais, en rapprochant les moyennes en pourcentage de sortie des chiffres, nous pouvons approcher sans nul doute d’un aléatoire de sortie. Outre, les écartypes standards entre les chiffres et les nombres lors de leur sortie confirment par exemple que le 12 sera souvent accompagné d’un nombre avec un écartype variable sur le panel de 11 à 12 et chaque chiffre ou nombre le confirme; Maintenant, la probabilité reste comme la combinaison, un attrape nigaud. pour ma part, par deux fois mes expériences à un chiffre prêt ont apportée une vérité très relative puisque deux cents autres n’ont pas étayées mes constats.. Que chacun soit conscient que l’impôt qu’il pait au jeu est une manière de penser pour nos dirigeant, que vous pouvez encore plus vous faire étrangler par l’impôt direct ou indirect. Arrêtez de jouer et penser à votre vie sociale pour l’améliorer.
J’aimeJ’aime
La moyenne de la somme d’une combinaison, n’est pas 20, elle est de ((50+1)/2)x5 = 127.5
J’aimeJ’aime
Quel bel article!
J’apprécie énormément votre capacité à expliquer simplement des choses qui sont plus complexes qu’elles en ont l’air.
Cordialement,
Pierre Lecomte
J’aimeJ’aime
Merci Pierre pour ce commentaire flatteur !
J’essaye autant que faire se peut de rendre chaque article le plus compréhensible possible, même si ce n’est pas toujours facile je l’admets !
J’aimeJ’aime
Limpide, merci beaucoup pour ces éclaircissements !
Pour approfondir votre démonstration concernant le nombre de tirages théoriques au bout desquels un numéro est censé apparaître à nouveau (10 fois), on pourrait s’intéresser au nombre de tirage nécessaires pour que l’ensemble des boules ait chacune été tirées au moins une fois, autrement dit le temps de réapparition de l’ensemble des boules. Intuitivement on pourrait penser qu’il faille 50 tirages…s’agissant de la démonstration je pense que c’est plus compliqué, mais que la formule du crible pourrait nous aider. Qu’en pensez-vous ?
Cordialement,
E.
J’aimeJ’aime
C’est une question intéréssante, elle me fait penser au problème du collectionneur de vignettes:
http://fr.wikipedia.org/wiki/Probl%C3%A8me_du_collectionneur_de_vignettes
Eljj avait fait un article amusant sur ce problème:
http://eljjdx.canalblog.com/archives/2013/01/27/26251336.html
En appliquant les formules données dans ces articles, et en considérant qu’un tirage Euromillion correspond à 5 tirages successifs, je trouve qu’il faut en moyenne 45 tirages Euromillion (c’est-à-dire 225 boules tirées) pour voir apparaître tous les numéros !
J’aimeJ’aime
Moins technique mais plus marrant
J’aimeJ’aime
Bonjour
Bon j’ai compris que je n’avais aucune chance de gagner 😉 (Et merde, ch’rais pôvre toute ma vie !) mais voilà, la probabilité qu’il y a une planète comme notre bonne vieille Terre est quasi nulle et pourtant elle existe (enfin je crois mais peut-être que nous ne sommes qu’un rêve éveillé d’un Dieu ?) . La probabilité de gagner à Euromillion est tout aussi nul et pourtant il y a régulièrement des gagnants….
Alors que faire ?
Je sais qu’en jouant ( de temps en temps, pour me donner de l’espoir d’ailleurs) , j’enrichis un Etat qui ne veut pas prendre aux plus riches mais peut-être qu’un jour…
En tout cas merci pour votre/vos démonstrations ; même si j’ai là un peu de mal ; il y a longtemps que je n’ai fait de proba et de maths aussi poussé. Ca doit remonter à près de 30 ans lorsque j’étais en IUT … et depuis mes bouquins de maths sont bien rangés.
Alain
J’aimeJ’aime
Bonjour. Enfin une analyse beaucoup plus pertinente que tout ce qu’on a l’habitude de voir. Cependant, j’ai toujours une question à laquelle je ne trouve pas de réponses et pour laquelle mes compétences en math et statistique sont beaucoup trop limitées.
La probabilité théorique de gagner est de 1/116 531 800 car il y a théoriquement 116 531 800 combinaison possible. Est-il possible de calculer le nombre réel de combinaison plausible en éliminant certaines combinaisons au caractère exceptionnel ? Je pense notamment aux combinaisons dont les 5 chiffres se suivent, ce genre de combinaison me parait impossible à tomber.
Merci d’avance pour votre réponse.
J’aimeJ’aime
Bonjour,
Ce qu’il faut comprendre, c’est qu’il n’y a aucune combinaison exceptionnelle. La combinaison 1-2-3-4-5 possède autant de chances de sortir que la combinaison 12-19-26-31-44.
En revanche, la probabilité de l’événement « la combinaison sortie est composée 5 nombres qui se suivent » est bien sûr plus petite que la probabilité de l’événement « la combinaison qui sort n’est pas du type « 5 nombres consécutifs » « , tout simplement parce qu’il n’y a que
5146 combinaisons qui sont composées de nombres successifs. Ce sont:1-2-3-4-5
2-3-4-5-6
3-4-5-6-7
…
46-47-48-49-50
Il y a donc une subtilité à bien comprendre ici.
Mais je le répète, la combinaison 1-2-3-4-5 possède bien autant de chances de sortir que n’importe quelle autre combinaison !
J’aimeJ’aime
donc si je suis bien il n’y a pas 51 combinaisons qui sont composées de nombres qui se suivent mais 46 !!??
J’aimeJ’aime
En effet, cela fait bien 46 séquences et non 51… Autant pour moi !
J’aimeJ’aime
1 chance sur 116 531 800, ce qui ceut dire: En jouant 5 combinaisons par tirage, cela arriverait en moyenne une fois tout les 224.099 ans et si 12 heures représentent les 116 531 800 combinaisons, alors le nombre de combinaisons déjà sortie représente 0.4 seconde, donc il reste 11h59min59sec 6/10 pour le reste des combinaisons à venir
J’aimeAimé par 1 personne
Bonjour,
Tu es stupide parce que tu fais des math pour des math. Sache que les boules ne sont pas toutes égales en masse, et que toutes n’ont pas les même chance de sortir !
Celles qui sortent le plus souvent ce n’est pas un hasard, c’est une réelle conséquence physique d’un calcul hautement complexe, prenant en compte leurs masses respectives et le module de mélange, ainsi que la position du trou.
Bref tes statistiques qui considèrent chaque boules physiquement identiques et physiquement en un même endroit de l’espace, ne valent rien du tout.
J’aimeJ’aime
C’est vous qui êtes complètement stupide, aucunes ne sortent plus souvent qu’une autre ni moins, la moyenne sera toujours équilibrée, et si l’une ou l’autre est 1/1000 de gramme plus lourde ou légère ne change rien dans la logique même.
J’aimeJ’aime
A noter qu’il y a plusieurs jeux de boules différentes. du coup des statistiques / estimations incluant la masse des boules ne sont applicables que si l’on connais la série utilisée à chaque tirage et cette dernière est elle-même tirée au sort par l’huissier au début du tirage, et bien-sûr FDJ ne diffuse pas cette info 😉
J’aimeJ’aime
parfaitement d accord trop de theorie mais il faut bcp de » chance michel
J’aimeJ’aime
il serait quand même bon de souligner que les gagnants des loteries ne sont en général ni des matheux ni des statisticiens …..alors finalement à quoi bon tout ça? :))
J’aimeJ’aime
Impossible de prévoir mathématiquement les résultats, on sait juste que la somme moyenne d’un tirage est forcément de( (1+45)/2)x6 = 138.
J’aimeJ’aime
Moi je me suis toujours dis que celui ou celle qui a reussi a gagner les millions et meme les dizaines de millions, c’est pas que c’est un chanceux.. C’est juste qui ont comprit le délire de l’euro million, il ne faut pas simplement jouer en sacharnant sur des numeros mais bien comprendre, etudier et tenter une combinaison utile..
J’aimeJ’aime
Lool réveilles vous aucun calcul ne peux trouvez la combinaison la théorie la plus simple est que, 1: la fdj c est l’etat 2: les pays européen vende du rêve aux petits ouvrier , chaque pays de l’europe prend ces petits milion chaque soir d’un tirage on va dir que ce sont les budjets pour les politicien leur confort sécurité hôtel chauffeur
J’aimeJ’aime
Lool réveilles vous aucun calcul ne peux trouvez la combinaison la théorie la plus simple est que, 1: la fdj c est l’etat 2: les pays européen vende du rêve aux petits ouvrier , chaque pays de l’europe prend ces petits milion chaque soir d’un tirage on va dir que ce sont les budjets pour les politicien leur confort sécurité hôtel 10 étoile lol chauffeur et j’en passe brf et il existe de gigantesque serveur que peu de gens save ou il sont qui permette de comptabiliser et sortir les numéro les moin jouer ensuite il ne faut pas être un fin stratège pour comprendre que le pseudo tirage sur tf1 est truquer que les boules ne coince jamais et quelle sont automatiquement attirer dans le trou »’ensuite si gagnant ya » enfin le front monetair international decide d’injecter ces million la ou bon leur semble de préférence dans une région retraité pour qu’un banquiers scrupuleux fasse des investiment à tort et à travers et n’oublions pas que le principale beneciair sera la mairie ,je ne dit pas que les math ne serve à rien bien au contraire des fois il suffit d’être juste réaliste ‘et enfin posez la question à la fdj pour quel raison ne pouvons nous pas valider nos tiquet à 5minute avant le début du tirage comme sur les match de foot.
J’aimeJ’aime
samir prenez des ciurs d orghographe
J’aimeJ’aime
Essayez d’écrire l’arabe au niveau de son français déjà, et restez tolérant, c’est quelqu’un qui essaie de communiquer comme il peut en restant poli. Merci pour lui.
J’aimeJ’aime
Bonjour,
Tout d’abord, je vous félicite pour cet article si bien expliqué qu’il en est tout simplement clair.
Si j’ai (à ma grande joie) « atteris » sur votre blog c’est parce qu’en regardant les numéros sortis hier soir donc le mardi 19 janvier 2016 qui étaient les suivants : 2 30 38 43 46, et en les comparant avec ceux sortis au tirage précédent donc le vendredi 15 janvier 2016, qui eux sont : 10 19 38 43 46 o.O
Et je me suis donc demandé qu’elle probabilité il y avait pour que cela arrive ?
Je ne suis malheureusement pas une « pro des maths » nous dirons et je me suis dis, en vous lisant, que si quelqu’un pouvais avoir la réponse et me l’expliquer en prime c’était vous !
Zhell.
J’aimeJ’aime
Il n’y a pas plus de probabilité qu’un tirage sorte plus qu’un autre, donc 1 chance sur 116 531 800 ou alors qu’un tirage précis sorte 2x de suite (116 531 800) exposant 2 soit 1 chance sur 13579660410000000
J’aimeJ’aime
Mouarf tant pis mais ça manque tellement de fantaisie tout ça
Merci pour la réponse et bonne journée 🙂
J’aimeAimé par 1 personne
Tout d’abord merci pour vos compliments. Je suis content de voir que cet article est clair et qu’il a apporté des réponses à vos questions.
Pour répondre à votre question, il faut faire un petit dénombrement. Si je résume votre question: sachant que la grille gagnante cette semaine est 2 30 38 43 46, est quelle est la probabilité que la grille gagnante la semaine suivante contienne les trois numéros 38, 43 et 46 ?
Pour cela, il suffit de dénombre toutes les grilles qui contiennent ces trois nombres. Elles sont de la forme X Y 38 43 46, où X et Y sont deux nombres à choisir parmi tous les entiers de 1 à 50 (sauf 38, 43, et 46). Il y a donc autant de telles grilles que de façons de choisir deux nombres parmi 47.
La probabilité cherchée est donc de .
.
Cela dit, il s’agit de ce qu’on appelle une probabilité conditionnelle (« sachant que… »). La probabilité (absolue) que la grille 10 19 38 43 46 sorte le 19 Janvier était bien de 1/116 531 800 donc environ 0,000000008.
J’espère que cette réponse vous éclairera un peu plus (même s’il y a quand même beaucoup de choses subtiles en probabilités !)
J’aimeJ’aime
Et ne me répondez pas « autant que les autres » s’il vous plaît je trouverais ça trop triste …
J’aimeJ’aime
Complètement absurde, même si une boule ne sort plus pendant 70 tirages, elle sortira en moyenne comme les autres 1xsur10 puisqu’il y a 5 boules tirées sur 50 (50/5) = 10 , plus il y a de tirages et plus la moyenne se rapprochera de 10. On ne peut absolument pas calculer un tirage ou une partie de tirage à l’avance (0%)
J’aimeJ’aime
Il y a en tout: (50!/(45!x5!)) x (11!/(9!x2!)) = 2.118.760 x 55= 116.531.800 combinaisons.Si on joue 10 combinaisons par semaine il faudra en moyenne 224.000 ans pour gagner et en ayant joué: 233.063.600 Euros, maintenant en ne se basant que sur les 5 boules comme vous dites sans tenir compte des 2 étoiles, alors 2.118.760 combinaisons et 96% de chance de gagner: soit jouer 2.034.009 combinaisons ou 4.068.018 euros pour avoir un 5 soit en moyenne récupérer:4000 euros
J’aimeJ’aime
Si on lance une pièce, il n’y a pas tout à fait 1chance sur 2 pour qu’elle retombe sur face ou pile car il y a le tranchant, plus le rapport diamètre/ tranchant est petit, plus il y a de chances qu’elle retombe sur le tranchant, 1 pièce de 1ct a donc plus de chance qu’une de 2 euros, environs 1x sur 500.
Ce qui veut dire pour avoir une idée de gagner à Euro million (1 chance sur 116 531 800), il faudrait qu’une pièce de 1 ct retombe sur le tranchant environs 3x de suite ( 500 exp 3 = 125 000 000 )
Cela arriverai, une fois tout les 2.240 siècles à raison de 5 lancés de pièces pour un tirage d’euro million.
Si on lance cette pièce toutes les 15 secondes il faudrait environs 58 ans.
A Euro million (1 chance sur 116 531 800), si on joue 5 combinaisons par tirage, il faudrait donc attendre en moyenne 224.099 ans pour gagner ou 2.240 siècles en ayant joué: 233.063.600 euros
J’aimeJ’aime
Il n’y a pas de méthode, aucune combinaison n’ est favorisée par une autre, chacune à forcément une chance sur 116 531 800 soit une fois tout les 224.099 ans, c’est la seule chose qu’on sait dire.à part que la moyenne de la somme d’un tirage est de 127.5. Plus on regarde de sortie de tirage et plus la moyenne se rapproche de 127.5, logique puisque ((1+50)/2)x5 = 127.5
J’aimeJ’aime
Bonjour. Merci pour l article.Je ne comprend pas pourquoi une explication compliquée (Chaîne de Markov) est nécessaire pour démontrer que chaque numéro apparaît une fois sur dix: Il y a 5 balles de tirées sur 50. C est à dire 1 chance sur 10. Voilà tout. Non?
J’aimeJ’aime
En mathématiques, il faut tout démontrer, même ce qui paraît évident ! 😉
J’aimeJ’aime
Exactement, mais certains aiment compliquer les choses logiques
J’aimeJ’aime
Il ne faut pas l’écart type pour calculer une moyenne, c’est comme un lancé de dé à jouer, c’est une suite arithmetique (1+6)/2 = 3.5. Mes calculs sont exacts et on ne pourra jamais analyser ni prévoir une seule combinaison. Pour avoir 4% de chance perdre, il faut donc 96% de chance de gagner et si c’est pour gagner uniquement en se basant sur un »5 » sans les étoiles, on est très largement perdant puisqu’il y a 2 118 760 combinaisons et (96%) représente 2 034 009 ou 4.000.000 d’euros à jouer pour en gagner en moyenne 4000 seulement et cela dans une période de 41 siècles. C’est une perde de temps totale et logique d’essayer de trouver une méthode à ce jeux, tout les statisticiens savent ça.
J’aimeJ’aime
Je vous prie de bien vouloir arrêter de polluer les commentaires avec vos multiples copier/coller.
Vos commentaires, en plus d’être encombrants, n’ont pas beaucoup de sens mathématique (et parfois pas de sens du tout), donc je les laisse encore quelques heures puis je les supprimerai purement et simplement. Merci de votre compréhension.
J’aimeJ’aime
Exactement, on ne peut prévoir aucunes sorties d’avance, chaque boule a 1/10 (50/5) de sortir et la moyenne est de 127.5 ( (1+50)/2)x6 C’est tout ce qu’on peut dire avec euromillion. On peut écrire 200 livres pour essayer de faire croire aux gens qu’on peut prévoir certaine sortie, ça ne sert à rien du tout, c’est aléatoire. Dans ce cas pas besoin d’écart type puisqu’il est fixe comme la moyenne :127.5 . L’écart type c’est pour: exemple: moyenne des points à un examen ou moyenne des températures relevées mais pas pour le loto ni un lancé de dé ou de pièce. Il sera forcément toujours le même d’autant plus de tirage il y a.
J’aimeJ’aime
Noaie a un livre à vendre à des incrédules, aucunes statistiques n’est possible avec le hasard, c’est comme la roulette ( rouge 18/37) ou un lancé de dés (1/6) ou d’une pièce (1/2), tout les matheux savent ça, c’est logique. loto ( 5/50)
J’aimeJ’aime
Est-il exact que les 50 boules n’ont pas la même masse? Ont-elles été pesées avec une très grande précision ? Est-il exact que la FDJ utilise plusieurs jeux de boules et non un seul ?
Après 967 tirages les 5 boules qui sont les plus et les moins sorties dans le trou sont avec les 2 étoiles
14 19 38 44 50 2 8
2 31 32 41 46 4 6
Avec des quotients qui ne cessent de se différencier
37,20 382
45,69 299
564 383
47,26
Pourquoi le quotient cinq meilleures sorties/ Cinq moins biens sorties ne cesse d’augmenter ?
J’aimeJ’aime
Bonjour,
Merci pour cette demonstration. Il est certain que la maîtrise des maths n’aidera pas a deduire la prochaine combinaison. Rien ne sert d’essayer. J’ai vu des expert du developpement informatique éditer en masse des feuilles de loto basé sur des theories mathématiques.Ils mangenet encore des patates aujourd’hui.
Pour autant, depuis que je me base sur les sites de stats de jeu, je me fais systématiquement rembourser la mise à minima. C’est peu mais ça me distrait. Je n’arrive pas à expliquer la sortie des numéros restants…. putain de loi binomiale!!!! 😉
Merci encore
J’aimeJ’aime
Il y a également des vérités non mathématique basées sur l’observation. Les tirages précédents influencent les résultats précédents, les nombres consécutifs, probabilité d’avoir un tirage dans la même dizaine….
J’aimeJ’aime
Et Bayes dans tout ça?
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Bayes
J’aimeJ’aime
un petit tableau
1 2 3 4 5 10 15 20 23 30 32 38 44 49 (nb boules sélectionnées)
1 10 19 28 35 42 69 85 93 96 99 100 100 100 100
2 1 2 4 7 26 48 67 77 92 95 99 100 100
3 0 0 0 5 15 31 42 69 76 92 99 100
4 0 0 0 2 8 13 33 40 65 90 100
5 0 0 0 1 2 7 10 24 51 90
(nb boules sortantes)
si je sélectionnes 30 boules parmi 50.
j’ai 99% de chance d’avoir 1 boule gagnante, mais seulement 7% que j’ai bien 5 boules gagnantes
si je sélectionnes 38 boules parmi 50.
– j’ai 99% de chance d’avoir 1 boule gagnante
– j’ai 92% de chance d’avoir 2 boules gagnantes
…
– je n’ai que 25% d’avoir les 5 boules gagnantes
pourquoi les gagnantes comme Richard Lustig conseille
– de prendre une série de nombre
parce que si il choisit 38 boules au lieu de 50 à jouer, 25% du ‘temps’ il aura raison.
Attention prendre 38 boules signifie que l’on a 25% de l’ensemble des combinaisons à 5 boules parmi 50.
– de suivre les boules sortantes
il est rare d’avoir des numéros d’une même semaine sortir
~0% de chance que la combinaison ressorte, mais 42% d’avoir 1 boule qui ressorte, 7% pour 2.
J’aimeJ’aime
un petit tableau
……1…..2…..3…..4…..5….10….15….20….23….30….32….38….44….49 (nb boules sélectionnées)
1….10….19….28….35….42….69….85….93….96….99…100…100…100….100
2………..1…..2…..4…..7….26….48….67….77….92….95….99…100….100
3……………..0…..0…..0…..5….15….31….42….69….76….92….99….100
4…………………..0…..0…..0…..2…..8….13….33….40….65….90….100
5………………………..0…..0…..0…..1…..2…..7….10….24….51…..90
(nb boules sortantes)
J’aimeJ’aime
et dieu dans tout ça.
pour l’instant il est très occupé au moyen orient, là ou il est né.
je continuerai à jouer les N°de ma première bourre combinée à sa datte (qui était NOUR) de naissance en dégustant une bière avec quelques potins de comptoir et on attend de voir….
avec cette façon de faire j’ai raté de peu 400.000€ au tirage du 6/05/2016 j’ai jouer 44 au lieu du 40.
bonne chance à tous. que deviendront nous sans rêver un peu – la preuve les scientifiques continuent toujours de rêver ils décrochent la lune – mars – rosétta etc….nous sommes nous pas le fruit du hasard, je le pense…dieu n’est pas mort puisqu’il n’a jamais existé.
seulOmonde
J’aimeJ’aime
très bien fait cet aritcle les proba n’ont jamais étaient ma tasse de thé..Je prefere laisser au pro ..
J’aimeJ’aime
Une petite pour la route, au loto en 1995 ,cela ma pris comme ça ? j’ai selectionner les 9 Nos les + sortis en realisant 111 grilles en jeu simple , a la 3eme semaine de validation du mercredi , les 6 bons Nos etait dans la selection , j’ai rater 1.100.000 millions. – Mon collegue m’avait dit que je pouvais les jouer sur 1 ticket multiple (10Nos) je l’ais pas écouter , seul gain 5 Nos toucher et 14 fois 4 Nos – Depuis je ne joue plus.
J’aimeJ’aime
J’ais oublier de dire qu’ il y avait en + le No complementaire.dans la selection de 9.
J’aimeJ’aime
Je suis désolé mais je joue régulièrement car j’ai une chance sur deux de gagner à chaque fois :
Soit je gagne, soit je perds ! 50/50.
Quand la philosophie rejoint les maths (Je n’ai pas dit la sagesse, bien que l’étymologie le laisse entendre …)
J’aimeJ’aime
Si il y a 1 chance sur 2 c’est que forcément on joue la moitié du nombre de combinaisons dans cette tranche de gains, c’est mathématique.
J’aimeJ’aime
Je pense que l’on peut diminuer le nombre de combinaisons en regardant le nombre des probabilités fortes (idéalement a plus de 80%) qui ne sortent pas.
Par exemple si je prends les derniers tirages, les numéros de 50, et de 1 à 12, soit 13 boules.
Elles ne sont pas sorties dans les 3 derniers tirages
14 21 24 29 30
29 30 36 40 41
15 25 26 40 41
La probabilité pour avoir au moins une boule dans les 13 numéros est de 0.8 (soit 80% des combinaisons totales), donc 0.2 (20% des combinaisons totales) pour qu’il y en ait aucune des 13.
Pour cet événement se reproduise une 4 ème fois c’est une probabilité de 0.2^4, soit 0,0016.
idem pour les suites, on ~33% de chance d’avoir une suite, cela fait donc 3 tirages ou on a des suites (29-30, le 29-30 et le 40-41, le 25-26 et 40-41) donc le prochain tirage la probabilité d’avoir une 4 ème fois une suite est de 0.33^4 ~ 0.012.
Un autre indicateur qui pourrait arriver c’est les numéros de 38 à 49 (soit 12 numéros), cela fait 2 tirages de suites qu’il y a 2 boules qui sortent de cette liste. la probabilité d’avoir 2 boules qui sortent parmi 12 c’est 0.355, donc idem, pour que la liste ai encore 2 numéros qui sortent dans cette liste c’est 0.355^3 ~ 0.045, soit ~95% pour qu’il n’ait pas 2 boules dans cette liste.
on a donc
1 – indicateur: d’avoir au moins une boule dans la liste (50, 1,2,3,4,5,6,78,9,10,11,12) soit ~80% des combinaisons.
une probabilité des (1-2^4) ~ 0.99, d’avoir une boules dans la liste.
2 – indicateur: des suites, soit ~66% des combinaisons qui n’ont pas de suites
une probabilité de (1-0.33^4) ~ 0.99 de ne pas avoir de suite.
3 – indicateur d’avoir 2 boules dans la liste de 38 à 49, soit ~65% des combinaisons qui n’ont pas au moins 2 boules dans la liste (38,39,40,41,42,43,44,45,46,47,48,49)
une probabilité de (1-0.355^3) ~0.95 de ne pas avoir 2 boule dans la liste.
La probabilité totale que les 3 événements arrivent c’est 0.99*0.99*0.95 ~ 0.93.
pour un nombre de combinaisons totales de 80%*66%*65% ~ 35%
J’aimeJ’aime
Le raisonnement serait valable si le tirage n’est pas pipé…
Lire 1984 pour comprendre.
J’aimeJ’aime
Il n’y a pas de méthode à essayer de trouver une solution pour avoir plus de chance de gagner, ce ne sont pas des chevaux, ni des être humains, c’est complètement absurde de dire qu’on a trouver une méthode.
J’aimeJ’aime
Oui et non, à l’infini, tous les numéros sortent dans les mêmes proportions.
J’aimeJ’aime
mrtaz42, tu parles du livre 1984 de George Orwell ?
je ne pense pas que les boules soient pipées, les statistiques rejoignent les probabilités, l’exemple de la liste 50, 1..12 ci-dessous montre une bonne mesure des tirages.
Michel, je pense que l’on peut pas prendre toutes les probabilités même forte en compte on pourrait vite arriver a une probabilité du style 0,98x 0,99x…x0,95 ~ 0,01.
j’ai vérifié c’est déjà arrivé que 4 tirages de suite n’ai pas de boules (50, 1,.., 12).
21 24 31 39 47
13 15 20 24 46
13 21 24 44 49
18 23 26 35 44
c’est le seul cas sur les 750 derniers tirages.
on a (157/750) qui ne sortent pas soit 20%, sur ces 157, 20% des 157 sorties simples redonnent des doubles, puis 20% des triples …
bref pour le moment on 4 cas ou on a des triples, et un cas de quadruple, en avoir un second maintenant ça parait en avance, mais c’est possible.
en tout cas aucun quintuple.
Donc pour moi c’est juste un moyen de trouver des combinaisons qui me paraissent plus crédible.
J’aimeJ’aime
Avec ma méthode j arrive à trouver le Nr qui va sortir seulement c est très lent il faut du TPS bcp de cassements tête. Voilà les Nr des combinaisons sortis se suivent les compter en diagonal j arrête là car c est long à expliquer et je suis très sérieuse pour ce que je viens de dire. Les Nr se suivent.
J’aimeJ’aime
Absurde.
J’aimeJ’aime
Résultats Euro Millions. Android app: https://play.google.com/store/apps/details?id=lapt0pd0g.lotteries
J’aimeJ’aime
Bofff
J’aimeJ’aime
C » est très ennuyeux pour un jeu qui devrait juste nous amuser ! Les humains cherchent bien des complications où il n’y en a pas 🙂
J’aimeJ’aime
Trop compliqué l’euro million,je vais me faire un petit loto ,hi,hi,hi…
J’aimeJ’aime
Magnifique !
EXCELlente démo !
…dans la joie
Merci
Le website mentionné ci-après va fonctionner en mars 2018
J’aimeJ’aime
Pour celles et ceux qui ne pourraient pas s’abstenir de jouer malgré la brillante démonstration, un conseil supplémentaire:
– Jouez au hasard (en essayant éventuellement de deviner les combinaisons les « plus rentables » comme expliqué dans l’article). C’est à dire ne vous attachez pas à des numéros ou à des séquences, changez à chaque fois et oubliez!
Vous perdrez sûrement votre argent mais vous pourrez arrêter ou oublier de jouer sans perdre la raison, ce qui serait quand même plus grave…
J’aimeJ’aime
Ce qui est Formidable c que vue la probalité trés trés faible de gagner…voire impossible…
Et vue le tout petit nombre de joueur qui existe environ 40 000 000 de joueur en moyenne ? Sachant que les joueurs ne communiquent pas ensemble pour optimiser leur combinaisons et
avoir plus de chances d’avoir au moins un grand gagnant .Sachant que les joeurs joue souvent tous les méme numéro ce qui augmente donc encore plus l’impossibilité d’avoir un gagnant.
Vue que le nombre de grille possible est 116 531 800 ? si j’ai compris qque chose. Pourquoi il y a des gagnants aussi souvents ? Il ne devrais y en avoir bcp moins ? Non ? Peu t’on mettre en évidence statistiquement pourquoi il y aussi souvent des gagnants remportant de gros jackpot ? Le jeu parait vraiment truqué..
116531800 / 40 000 000 = 2,913295.. soit environ un gagnant tout les 3 tirages si chaque grille joué est unique …ou trés peu de redondance entre les grilles joué…donc ?
Statistiquement est ce normal d’avoir autant de gagnants ?
Merci 🙂
J’aimeJ’aime
Vous calculez seulement pour une combinaison par personne, alors que les gens en jouent plus, donc forcément, il y a plus de gagnants que 1 sur 2.9.
J’aimeJ’aime
Ah bon les joueur ne son pas comptabilisé a la mise ?
1 combinaison acheté une mise compté = un joeur… ?
J’aimeJ’aime
Ca dépend de quoi on parle, je vois qu’il y a en moyenne 26.000.000 de combinaisons jouées par tirage pour 3.000.000 de personnes, donc 116.000.000 / 26.000.000 = 4.46; 1 x sur 4.6 une combinaison sortira au rang 1 en moyenne. Mais 8 combinaisons de moyenne par personne ( 26.000.000 / 3.000.000 ) donc moins de personne forcément.
J’aimeJ’aime
Merci pour la réponse.
Donc si je comprend qqchose… il devrais en gros y avoir 1 x sur 0.5 combinaison au rang 1 en moyenne. ( 4.6 / 8) ?. Donc 2 rang 1 pour chaque Tirage ??? Donc en fait c le contraire il n’y a pas autant de gagnants qu’il devrais y avoir ???
J’aimeJ’aime
salut a tous
Je vais vous decevoir car le loto et euromillion sont truqués!!
vous pouvez jouer toutes les combinaisons et la seule que vous ne jouerez pas sortira!!
c’est une arnaque
J’aimeJ’aime
Alors ne joue que celle la.
J’aimeJ’aime
loto et euromillion sont truqués
J’aimeJ’aime
Bonjour, décidément mes quelques neurones ne comprendront jamais rien aux mathématiques mais merci pour cette brillante démonstration fort intéressante. bon j’ai bien compris qu’il me faudrait vivre plusieurs siècles pour avoir une chance de gagner au premier rang. Pfffff… ça va être long mais tant pis je persévère quand même !
J’aimeJ’aime
Cet article est très intéressant, et vos connaissances en mathématiques et probabilité méritent des éloges. Les probabilités, il me semble, sont une question de bon sens. Il y a en outre, les questions qui relèvent de la physique. Le calibrage des boules, la rotation de la sphère, les divers obstacles que les boules rencontrent et avec lesquelles elles s’entrechoquent, l’ordre d’introduction des boules dans la sphère, les différences éventuelles entre jeux de boules, la durée de rotation de la sphère avant l’ouverture de la trappe, etc… etc… ce qui nous laissent penser à une totale incertitude de tirage et donc à une combinaison gagnante véritablement aléatoire. Pour autant la qualité de cet « aléatoire » sans être mise en doute comme je l’ai lu dans un commentaire, me semble suffisamment satisfaisante pour que l’échantillonnage de probabilité soit « valide » ou « validable ». Des millions de personnes jouent à l’Euro-millions sur notre planète, et bien souvent plusieurs jeux simples ou multiples, pour autant, malgré cela, les tirages avec remise du jackpot se succèdent… Le prochain sera de 176 millions… Une énorme carotte sur la lune… Elle est visible à l’œil nu et il faudra avoir un sacré trampoline pour l’attraper. Pourtant quelqu’un va le faire !!! (j’ouvre ici une parenthèse, je suis prof d’Arts Martiaux et non mathématicien, et je m’adonne à l’écriture, il m’arrive parfois d’imaginer (le propre des écrivains étant l’imagination…), que tout ce système serait une grande arnaque et que personne ne puisse réellement gagner. Et que les seuls gagnants seraient des personnes choisies par les organisateurs pour couvrir leurs agissements… un peu comme les « fameux barons » – complices de l’arnaque… bref, un beau délire…) je referme la parenthèse…
J’en viens donc au fait qui taquine mon bon sens. Malgré que je sois conscient de l’indépendance des tirages, je suis, également un expérimentateur. Je sais que la combinaison 1-2-3-4-5 a autant de chances de sortir que les autres, et ceci même pour ce prochain tirage !!! Je sais aussi, que la combinaison qui pourrait s’enchaîner lors du tirage suivant pourrait aussi être 6-7-8-9-10 ! et ainsi de suite. 🙂 Je ne vais pas m’amuser à essayer de calculer la chance de sortie d’une telle option. Malgré que les deux soient tout à fait possibles dans l’absolu. Je crois qu’on parle là de conditions improbables… voir TRES TRES IMPROBABLE (surtout sur un petit échantillonnage), mais pas impossible ! Vous commencez votre article avec ces deux affirmations courantes que vous décortiquez par la suite de façon captivante et logique :
a) Il y a des numéros qui ont plus de chances de sortir que d’autres;
b) Si un numéro n’est pas sorti depuis longtemps, alors il a plus de chances de sortir au prochain tirage.
La première assertion, est bien sûr, une assertion qui semble contredire l' »aléatoire » des tirages, et celle là me paraît être, dans notre cas, absolument pas fiable.
La seconde assertion est beaucoup plus intéressante : Plus l’échantillonnage étudié sera suffisamment grand et plus il nous sera possible de la vérifier. Or, en la vérifiant, j’ai pu commencé d’observer une sorte de logique de bon sens. Je pense que si nous avions plus de TEMPS et d’ARGENT à consacrer à cette aventure, nous pourrions réduire dangereusement le champ de ratissage de la Française des jeux…
J’aurais peut-être le temps de vous recontacter après le prochain tirage, mais ce n’est pas sûr, car j’ai prévu de gagner et cela va impliquer une totale ré-organisation !!!
à bientôt j’espère
et encore Bravo pour votre travail
J’aimeJ’aime
Suffit de voir certains tirages avec des suites genre 29-30 ou 7-8 ou 14-15 et comme par hasard il n’y a pas de gagnants. Je soupconne fortement la FDJ de modifier le tirage avec des boules truquées reliés à un ordinateur qui choisi les numéros qui ne pourrons pas correspondres au millions de grilles jouées. evidemment très peu de personnes font des suites de chiffres et la probabilité d’avoir cette combinaison precise est très très faible donc la FDJ n’a plus beaucoup de choix et doit faire des suites pour ne pas avoir de gagnants. Voilà pas besoin de faire de savant calculs mathematique c’est juste du bon sens !
J’aimeJ’aime
Merci pour toutes ces précisions solidement argumentées … la répartition des gains mérite également un commentaire : pourquoi un gain avec une bonne étoile et zéro numéro, et pas de gain avec une bonne étoile et un bon numéro ??
J’aimeJ’aime
Ping : L’esprit européen | MGA33