– T’as vu la nouvelle horloge que je me suis achetée ?
– Nan, fais voir !
– Tiens, regarde:
– Trop cool !
– Mince, il est déjà 10h31, je suis en retard !
Fin de l’histoire. Ok, là vous allez dire que cette histoire n’a aucun sens. Et je ne pourrai que vous donner raison SAUF pour l’horloge. Il existe bel et bien une horloge comme sur le dessin et qui donne vraiment l’heure ! On peut la trouver à Berlin. La voici:

Il est 10h31 (source: http://en.wikipedia.org/wiki/Mengenlehreuhr)
Pour l’anecdote, cette horloge a été inventée par un certain Dieter Binninger et elle fût installée pour la première fois en 1975 à Berlin.
Comme vous avez pu le constater, elle indique l’heure de manière plutôt étrange… Je vous propose d’essayer de comprendre son fonctionnement.
Explication du fonctionnement de l’horloge
Contrairement aux premières impressions, le principe de cette horloge n’a rien de bien sorcier. L’idée est la suivante: chaque lampe allumée indique qu’une certaine durée de temps s’est écoulée. Plus précisément:
- Chaque lumière de la première ligne représente 5 heures.
- Chaque lumière de la deuxième ligne représente 1 heure.
- Chaque lumière de la troisième ligne représente 5 minutes. (les lumières rouges indiquent les quarts d’heure)
- Chaque lumière de la dernière ligne représente 1 minute.
Par exemple, quelle heure indique l’horloge suivante ?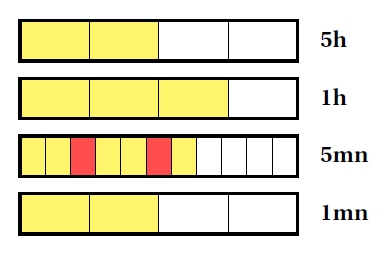 Eh oui, il s’agit bien de 13h37 ! En effet:
Eh oui, il s’agit bien de 13h37 ! En effet:
- deux lumières sont allumées dans la première ligne, donc cela donne 2x5h = 10h;
- trois lumières sont allumées dans la deuxième ligne, ce qui donne 3x1h = 3h;
- sept lumières sont allumées dans la troisième ligne, ce qui donne 7x5mn = 35mn;
- deux lampes sont allumées dans la dernière ligne, ce qui donne 2x1mn = 2mn.
Il suffit ensuite d’additionner le tout: 10h + 3h + 35mn + 2mn = 13h et 37mn !
Mais pourquoi cette horloge est une vraie horloge ?
A priori, rien ne dit que chaque temps de la journée peut être représenté à l’aide de cette horloge (existence), ni même que chaque configuration de l’horloge ne peut représenter deux heures distinctes (unicité).
Nous allons donc prouver mathématiquement que c’est bien le cas et, pour cela, nous allons commencer par tout convertir en minutes. Comme vous le savez, dans une journée il y a 24 heures, ce qui fait 1440 minutes. Ainsi,
- Chaque lumière de la première ligne indique que 5×60 = 300 mn se sont écoulées.
- Chaque lumière de la deuxième ligne indique que 1×60 = 60 mn se sont écoulées.
- Chaque lumière de la troisième ligne indique que 5 mn se sont écoulées.
- Chaque lumière de la dernière ligne indique qu’1 mn s’est écoulée.
D’autre part, chaque temps de la journée, si on l’exprime en minutes écoulées depuis minuit, est représenté par un nombre entier compris entre 0 et 1440. Par exemple, 2h34 = 94 mn après minuit et 20h10 = 1210 minutes après minuit.
L’horloge de Berlin marche grâce à la proposition suivante:
Tout nombre entier compris entre 0 et 1440 s’écrit de manière unique sous la forme:
où et
sont des entiers compris entre 0 et 4 (inclus), et où
est un entier compris entre 0 et 11 (inclus).
Le nombre donnera le nombre de lumières allumées dans la première ligne, le nombre
le nombre de lumières allumées dans la deuxième ligne, etc.
Nous allons donc démontrer cette proposition pour voir que l’horloge de Berlin permet bien d’indiquer chaque moment de la journée. Vous allez le voir, la démonstration est similaire à celle qui donne l’existence et l’unicité de l’écriture d’un entier en base .
Existence
Soit est un entier avec
.
1ère étape: On effectue la division euclidienne de par 300. On sait qu’il existe donc deux entiers
et
tels que:
Il reste à voir que est bien un nombre compris entre 0 et 4 inclus. Or, d’après la relation précédente,
. Mais:
donc
Comme est entier, nous voyons ainsi que
.
2ème étape: On procède de manière similaire, et on effectue la division euclidienne du nombre précédent par 60. Il existe donc deux entiers
et
tels que
De la même manière qu’à la première étape, on va utiliser le fait que pour montrer que
est un entier compris entre 0 et 4. Or,
et
donc:
Nous voyons ainsi que . D’autre part,
.
Vous voyez qu’en continuant ainsi les divisions euclidiennes successives, on arrivera à la propriété voulue…
3ème étape: On effectue la division euclidienne de par 5. Il existe donc deux entiers
et
tels que:
Cette fois-ci, nous allons voir que est compris entre 0 et 11 (inclus). En effet, on a
et comme
:
donc . De plus,
4ème étape: Pour finir, va-t-on faire la division euclidienne de par 1 ? Non ! (car faut pas déconner non plus, se lancer dans une division par 1 n’a rien de bien passionnant…). On va tout simplement poser
et comme on a vu que
, on a donc immédiatement
, ainsi que la relation
Exemple en pratique: La preuve précédente nous donne évidemment un algorithme de décomposition pratique, et voici par exemple comment on a décomposé 12h34 = 754 mn:
754 = 2×300 + 154 = 2×300 + 2×60 + 34 = 2×300 + 2×60 + 6×5 + 4
Unicité
Pour l’unicité, nous allons supposer que se décompose de deux façons différentes:
ce qui, en faisant passer certains termes de l’autre côté, nous donne l’égalité :
d’où:
(*)
Cela montre que l’entier est un multiple de 5. Mais, comme les nombres
et
sont compris entre 0 et 4 inclus, on a aussi les inégalités suivantes:
. Vous en connaissez beaucoup des multiples de 5 compris entre -4 et 4 ? Il n’y en a pas énormément… Pour ne rien vous cacher, le seul est 0 ! Cela veut donc dire que
et donc
.
L’égalité (*) devient alors:
et donc:
Et là, rebelote, on suit le même raisonnement que précédemment, en commençant par factoriser:
(**)
Et donc, est un multiple de 12, mais comme
, on en déduit que
. Puisque le seul multiple de 12 compris entre -11 et 11 est 0, on a donc bien
!
On reprend ensuite l’équation (**), qui devient:
d’où:
(***)
Bon, je pense qu’au bout de la troisième fois vous commencez à comprendre l’idée: est un multiple de 5 qui vérifie
, ce qui donne donc
. Et l’égalité (***) devient alors
d’où
.
Voilà pour l’unicité. Joli, non ?
Votre propre horloge de Berlin !
J’ai écrit un programme qui affiche l’heure (en temps réel) comme l’horloge de Berlin. Voici une capture d’écran:
 Ce programme a été écrit en Python, et s’il vous intéresse, le code est disponible dans le lien suivant: http://pastebin.com/6DCR9WQM
Ce programme a été écrit en Python, et s’il vous intéresse, le code est disponible dans le lien suivant: http://pastebin.com/6DCR9WQM
Note:
Une des raisons pour lesquelles nous avons pu faire cette décomposition est le fait que 1mn divise 5 mn, qui elles-mêmes divisent 60mn, qui elles-mêmes divisent 300mn. Pour ceux qui aiment les horloges exotiques, voici un article sur Arxiv (lien direct vers le pdf) qui reprend cette idée, avec 1mn, 6mn, 30mn, 2h=120mn et 6h=360mn, pour créer une horloge triangulaire, dont voici quelques beaux exemples:





C’est très amusant et étonnant! Je ne suis pas étonné par le résultat mathématique mais bien par sa mise en oeuvre publique!
Quant au résultat mathématique, on peut le comprendre dans le cadre de la théorie des systèmes de numération. L’utilisation de la division euclidienne pour trouver les chiffres successifs est une manifestation de l’algorithme glouton qu’on applique dans une vaste famille de systèmes de numération généralisant les systèmes de position. Dans ces systèmes, on remplace la suite des puissances de la base par une suite strictement croissante d’entiers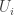 commençant par
commençant par  . Pour avoir un alphabet de chiffres fini, il faut et il suffit que le quotient
. Pour avoir un alphabet de chiffres fini, il faut et il suffit que le quotient  soit borné. Pour décomposer un nombre
soit borné. Pour décomposer un nombre 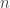 , on détermine
, on détermine 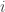 pour que
pour que  et on prend comme premier chiffre le quotient de
et on prend comme premier chiffre le quotient de 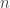 par
par 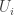 . Ensuite, on remplace
. Ensuite, on remplace 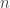 par le reste de sa division par
par le reste de sa division par 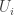 et on recommence. On intercale des
et on recommence. On intercale des 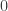 entre les premiers chiffres ainsi obtenus de manière que le rang de chaque chiffre soit celui de l'élément de
entre les premiers chiffres ainsi obtenus de manière que le rang de chaque chiffre soit celui de l'élément de 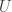 à l'aide duquel on a obtenu. L'algorithme glouton donne une décomposition canonique de chaque entier mais, en général, un même entier possède plusieurs décompositions comme combinaison linéaire des
à l'aide duquel on a obtenu. L'algorithme glouton donne une décomposition canonique de chaque entier mais, en général, un même entier possède plusieurs décompositions comme combinaison linéaire des 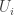 . Le système construit de la sorte avec la suite des nombres de Lucas s'appelle le système de Zéckendorf. Dans le cas de l'horloge berlinoise, les nombres 1, 5, 60, 300 peuvent être vus comme l'analogue de la base
. Le système construit de la sorte avec la suite des nombres de Lucas s'appelle le système de Zéckendorf. Dans le cas de l'horloge berlinoise, les nombres 1, 5, 60, 300 peuvent être vus comme l'analogue de la base 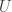 et les divisions successives réalisées pour coder une heure sont la manifestation de l'algorithme glouton.
et les divisions successives réalisées pour coder une heure sont la manifestation de l'algorithme glouton.
Une remarque pour finir : l'application qui associe à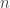 sa représentation dans la base
sa représentation dans la base 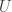 est strictement croissante quand on ordonne l'ensemble des représentations, vues comme des mots sur l'alphabet des chiffres, selon l'ordre généalogique. Cette observation est à la base de la création d'une vaste généralisation des systèmes de numération connus au moment de son introduction : les systèmes de numération abstraits. Ceux-ci sont étudiés depuis plus d'une dizaine d'années et ont donné lieu à de nombreux résultats importants dont des généralisations difficiles de deux théorèmes fondamentaux de Cobham. Pour une première approche de ces systèmes, je suggèrerais le chapitre 3 du livre : Combinatorics, Automata and Number Theory paru au Cambridge University Press en 2010.
est strictement croissante quand on ordonne l'ensemble des représentations, vues comme des mots sur l'alphabet des chiffres, selon l'ordre généalogique. Cette observation est à la base de la création d'une vaste généralisation des systèmes de numération connus au moment de son introduction : les systèmes de numération abstraits. Ceux-ci sont étudiés depuis plus d'une dizaine d'années et ont donné lieu à de nombreux résultats importants dont des généralisations difficiles de deux théorèmes fondamentaux de Cobham. Pour une première approche de ces systèmes, je suggèrerais le chapitre 3 du livre : Combinatorics, Automata and Number Theory paru au Cambridge University Press en 2010.
En tout cas, merci pour ce bel article!
J’aimeJ’aime
Merci pour ce commentaire très intéressant, Pierre !
J’aimeJ’aime
Ping : Animations diverses – scratchlouisemichel
merci vous m avez bien aidé
J’aimeJ’aime
De rien 🙂
J’aimeJ’aime