Formez la somme des quatre premiers nombres impairs: . Faites de même avec la somme des quatre nombres impairs suivants:
. Calculez alors la fraction obtenue en divisant la première somme par la seconde:
Le résultat est donc égal à . Magique, non ? Hum, non pas vraiment. Pas encore.
Recommencez ce que vous venez de faire avec, non pas la suite des quatre premiers entiers impairs et des quatre suivants, mais avec la suite des cinq premiers entiers impairs et des cinq suivants. Cela donne:
et on constate qu’on retrouve . Vous pouvez même essayer avec autant de termes que vous souhaitez, cela marchera encore:
Autrement dit, il semblerait que la somme des premiers entiers impairs soit toujours trois fois inférieure à la somme des
premiers entiers impairs suivants.
« L’important, c’est pas la chute… »
Ce résultat amusant, que vous venez peut-être de découvrir, est connu depuis au moins 400 ans (!) car il a été découvert par Galilée en 1615, alors qu’il travaillait sur la chute des corps.
Exprimée mathématiquement, voici ce que dit le la propriété trouvée par Galilée:
Pour tout entier naturel
,
Il existe une jolie preuve visuelle de ce résultat, que je ne vais pas commenter (puisqu’elle est visuelle !) et que voici:

Source: Nelsen, Roger B., Proof without Words: On a Property of the Sequence of Odd Integers (Galileo, 1615).
Une autre démonstration, plus calculatoire, est basée sur un résultat bien connu, à savoir que la somme des premiers entiers impairs est égale à
(voir un très vieil article de ce blog à ce sujet… ah, nostalgie) c’est-à-dire:
D’autre part, pour trouver la somme des nombres impairs suivants, il suffit de faire la somme des
premiers nombres impairs moins la somme des
premiers nombres impairs:
c’est-à-dire
On en déduit alors que:
Faites comme Galilée
Après avoir lu le résultat de Galilée, vous vous êtes peut-être demandé si cela marchait aussi avec les entiers pairs. Malheureusement, cela ne fonctionne pas du tout, car, par exemple,
Nous allons donc nous poser une question un peu plus générale: quelles sont les suites arithmétiques dont la somme des premiers termes divisée par la somme des
termes suivants est constante ? Pour cela, considérons une suite arithmétique
de raison
telle que la somme des
premiers termes divisée par la somme des
termes suivants soit toujours constante c’est-à-dire telle que pour tout entier
,
Avant de continuer, rappelons un petit résultat utile sur la somme des termes d’une suite arithmétique:
Si
est une suite arithmétique, la somme de
termes consécutifs de cette suite est égale à
fois la moyenne du premier et du dernier terme.
Autrement dit,
.
Grâce à ce résultat, on peut donc écrire que
Comme la suite est arithmétique de raison
, on sait alors que
. Ainsi,
A partir de là, on voit que le quotient de la somme des premiers termes par la somme des
termes suivants sera constant s’il existe un nombre
tel que pour tout
,
Cette relation est équivalente à
Autrement dit, si le quotient est toujours constant, alors la raison de la suite doit être égal à
.
Comme la raison de cette suite est une constante, elle ne dépend donc pas de , ce qui impose la condition
c’est-à-dire
.
A ce stade, on peut donc affirmer que si la somme des premiers termes d’une suite arithmétique divisée par la somme des
termes suivants est constante, alors cette constante est nécessairement
, comme dans la relation de Galilée !
D’autre part, comme , la raison de cette suite doit alors être
Autrement dit, la raison d’une telle suite doit être égale au double du premier terme. Cela était bien le cas avec la suite des nombres impairs car le premier terme est et la raison de la suite des nombres impairs est
.
Réciproquement, si une suite est arithmétique de raison
alors, en reprenant une égalité vue plus haut, on a
En simplifiant par au numérateur et au dénominateur, on obtient alors
Voici résumé ce que nous avons prouvé:
Soit
est une suite arithmétique de raison
.
Le quotient de la somme des
premiers termes par la somme des
termes suivants est constant si, et seulement si,
. Cette constante est alors
.
Avec cela, vous êtes maintenant capables de construire autant de suites « à la Galilée » que vous le souhaitez (si, si !). Par exemple, prenons la suite arithmétique de premier terme et de raison
(c’est-à-dire la suite dont les premiers termes sont
). Vous pouvez vérifier qu’on a bien
Magie !
Ce qui est bien avec tout ce qu’on vient de voir, c’est qu’on peut faire un petit tour de magie très facile car il ne vous demandera que de mémoriser un nombre: (ça ne devrait pas être trop dur… sinon, c’est que la magie n’est vraiment pas faite pour vous). Voici le tour:
- Demandez à une personne de choisir un nombre entier
au hasard mais sans vous le dire.
- Demandez-lui d’écrire sur une feuille la suite des nombres obtenus en partant du nombre
choisi au départ et en ajoutant
à chaque étape. Dites à cette personne qu’elle peut écrire autant de termes qu’elle souhaite de cette suite, du moment qu’il y en a un nombre pair
.
- Demandez-lui ensuite de couper la liste en deux parts égales, de calculer la somme des
plus grands nombres et de la diviser par la somme des
plus petits nombres de la liste, sans jamais vous donner le résultat (éventuellement à l’aide d’une calculatrice).
- Comme dans tout tour de magie qui se respecte, faites semblant de réfléchir et de calculer dans votre tête, tout en rigolant intérieurement.
- Annoncez-lui que le nombre obtenu est
.
- Ne répondez surtout pas à la question « Mais comment t’as fait, quoi ?« .
Par exemple, la personne choisit secrètement le nombre . Elle écrit sur sa feuille les
(nombre pair) premiers termes de la suite de nombres obtenue en partant de
et en ajoutant
à chaque fois:
La personne coupe alors sa liste en deux au milieu et fait la somme de chaque morceau:
et
Elle divise enfin la somme des cinq derniers termes par la somme des cinq premiers:
et vous lui annoncez alors qu’elle a trouvé !
Heureusement quand même qu’il y a des gens très sérieux qui ont utilisé les résultats de Galilée pour approfondir notre connaissance des lois de la Physique parce que si Galilée avait su que, 400 ans après, on utiliserait un de ses résultats mathématiques pour en faire un tour de magie foireux, pas sûr qu’il ait eu envie de continuer sa belle carrière de scientifique !
Notes et références:
- Nelsen, Roger B. “Proof without Words: On a Property of the Sequence of Odd Integers (Galileo, 1615).” Mathematics Magazine, vol. 68, no. 1, 1995, pp. 41–41.
- Stillman D. « Galileo Studies », University of Michigan Press, 1981, pp.218-219.
(dans lequel on apprend que Galilée avait déjà noté que la suite des nombres impairs est la seule suite arithmétique dont le premier terme vaut 1 qui vérifie la propriété vue dans l’article, à savoir que la somme despremiers termes est proportionnelle à la somme des
suivants.)
- John D. Norton, Invariance of Galileo’s Law of Fall under a Change of the Unit of Time
(dans lequel est expliqué le lien qu’à fait Galilée entre la somme des nombres impairs et le fait que la distance parcourue par un corps en chute libre est proportionnelle au temps). - Kenneth O. May, « Galileo Sequences, a Good Dangling Problem », The American Mathematical Monthly, Vol. 79, No. 1 (Jan., 1972), pp. 67-69.
(dans lequel est faite une étude des suites pas forcément arithmétiques qui vérifient la même propriété que celle étudiée dans cet article).


Il y a une petite faute de frappe dans le parenthèsage du dénominateur de la formule « r=\frac … »: il faudrait mettre (3k-1) au lieu de 3(k-1).
J’aimeJ’aime
Je viens de modifier cette erreur, merci de ma l’avoir signalée !
J’aimeJ’aime
OK bien vu Clem
J’aimeJ’aime
C’est amusant. Surtout que finalement, cela montre essentiellement l’unicité de la suite ayant la propriété de Galilée! En effet, si une suite a cette propriété, alors, en multipliant tous ses termes par une constante, on obtient une autre suite ayant cette propriété car cette constante disparait dans le quotient des sommes de deux suites consécutives de n termes consécutifs. L’unicité, si elle a lieu, s’entend donc à multiple non nuls près. Or, d’après ce que vous montrez, c’est en multipliant la suite des nombres impairs par une constante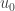 qu’on obtient touts les suites ayant la propriété de Galilée.
qu’on obtient touts les suites ayant la propriété de Galilée.
J’aimeJ’aime
Merci Pierre pour ces réflexions. Cela m’amène d’ailleurs à une autre: effectivement, si on multliplie une suite qui vérifie la propriété de Galilée par un réel, alors la nouvelle suite vérifie encore cette propriété.
En posant la relation d’équivalence où deux suites sont équivalentes si l’une est proportionnelle à l’autre, alors on voit effectivement que l’ensemble des suites arithmétiques dont la raison est le double du premier terme est une classe d’équivalence, dont un représentant est la suite des nombres impairs.
Je ne l’ai pas dit dans l’article, mais il existe cependant des suites qui ne sont pas arithmétiques et qui vérifient la propriété de Galileé (par exemple, la suite 1, 7, 19, 37… c’est-à-dire la suite telle que ). On peut donc se demander combien il y a de classes d’équivalence dans l’ensemble des suites qui vérifient la propriété de Galilée…
). On peut donc se demander combien il y a de classes d’équivalence dans l’ensemble des suites qui vérifient la propriété de Galilée…
J’aimeJ’aime
Ce qui est bien, dans l’exemple d’une suite non arithmétique vérifiant la propriété de Galilée, c’est que le rapport n’est pas On pourrait peut-être risquer une classification des classes d’équivalence avec ce rapport mais, ok, c’est prématuré à ce stade.
On pourrait peut-être risquer une classification des classes d’équivalence avec ce rapport mais, ok, c’est prématuré à ce stade.
J’aimeJ’aime
En fait, mais vous le savez sans doute, on peut déterminer toutes les suites ayant la propriété de Galilée. Soit une telle suite et
une telle suite et 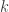 son rapport, supposé non nul. On considère la primitive
son rapport, supposé non nul. On considère la primitive  de
de  (elle n’est définie que sur les entiers strictement positifs). Alors, par définition
(elle n’est définie que sur les entiers strictement positifs). Alors, par définition  , ce qui donne
, ce qui donne 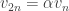 , où
, où 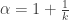 . Cela signifie que
. Cela signifie que  est connu si il l’est sur les nombres impairs. Autrement dit, les suites cherchées sont exactement celles définies par
est connu si il l’est sur les nombres impairs. Autrement dit, les suites cherchées sont exactement celles définies par  où
où  est une suite quelconque. Quant à
est une suite quelconque. Quant à  , il est donné par
, il est donné par 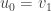 et, pour
et, pour 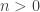 ,
, 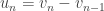 (c’est la dérivée de
(c’est la dérivée de  . Il reste encore un peu de travail pour l’exprimer efficacement en termes de
. Il reste encore un peu de travail pour l’exprimer efficacement en termes de 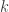 et de
et de  , avant de pouvoir éventuellement étudier les classes d’équivalence.
, avant de pouvoir éventuellement étudier les classes d’équivalence.
J’aimeJ’aime
Merci encore pour ce commentaire constructif ! Personnellement, je ne vois pas comment exprimer encore plus simplement après cela.
encore plus simplement après cela.
J’aimeJ’aime