Arnaquez vos amis à Pile ou Face

Avertissement: Blogdemaths décline toute responsabilité en cas de perte d’argent ayant été entrainée par la lecture de cet article. En poursuivant la lecture, vous acceptez qu’il est possible de perdre à un jeu de hasard, même quand les probabilités sont en votre faveur. Vous acceptez aussi de me faire don de la moitié de votre fortune personnelle.

Avant de commencer, j’aimerais mettre les choses au clair concernant le jeu de Pile ou Face: si vous lancez une pièce de monnaie bien équilibrée (non truquée, non pipée, tout ce que vous voulez), vous aurez toujours une chance sur deux de deviner le côté de la pièce qui sortira. Tout le monde sait ça. Alors comment donc arnaquer vos amis en jouant à Pile ou Face si on ne peut, de toutes façons, jamais changer la probabilité d’apparition de chacune des faces ?

Ce que tout le monde ne sait pas, c’est qu’il existe une variante de « Pile ou Face » qui, elle, est inéquitable. Et c’est ce que je vais vous montrer ci-dessous…

Place au jeu !

Le jeu auquel nous allons nous livrer est un jeu dans lequel deux joueurs vont s’affronter et qui va consister à lancer plusieurs fois de suite une pièce de monnaie. Avant la partie, chacun des joueurs choisit une séquence de 3 résultats (chaque résultat étant Pile ou Face). Puis, on lance la pièce de monnaie autant de fois qu’il le faut (en notant à chaque fois le résultat) jusqu’à ce qu’une des deux séquences apparaisse.

Par exemple, avant de commencer à lancer la pièce, le joueur 1 choisit la séquence PFP (Pile-Face-Pile) et le joueur 2 choisit la séquence FPP (Face-Pile-Pile). On lance ensuite la pièce plusieurs fois de suite et voici les issues obtenues successivement:

F P F F P F F F P P

Comme vous le voyez, cette partie a duré 10 lancers et la première séquence sortie est celle du joueur 2, qui est alors déclaré vainqueur. Bien sûr, vous pouvez pimenter la partie en décidant de mettre une petite (ou grosse) mise de départ, le gagnant remportant le pot…

Il y a $2^3=8$ choix possibles de séquences pour chaque joueur. A priori, le choixx des séquences est aléatoire, donc les deux joueurs devraient être censés avoir la même chance de gagner… en tout cas, c’est ce que l’intuition nous laisse penser. Mais nous allons voir que ce n’est pas le cas (d’où l’arnaque !), et surtout, nous allons essayer de comprendre pourquoi.

Une première simulation

Pour bien comprendre ce jeu et comprendre pourquoi notre intuition est mise en défaut, la première chose que nous allons faire est une simulation de partie.

Par exemple, on imagine que votre adversaire choisisse la séquence FFP et que vous choisissiez la séquence PFF. On imagine aussi que vous et votre adversaire ne soyez pas pressés et que vous décidiez de faire 10 000 parties (!). Précision: pour chaque partie, votre adversaire aura toujours la séquence FFP, et vous la séquence PFF.

J’ai simulé cette situation à l’aide d’un programme et voici les résultats obtenus à la fin des 10 000 parties:

Lors de cette simulation, votre adversaire a gagné 2526 fois et vous avez gagné 7474 fois. Autant dire que vous l’avez mis minable.

Vous constatez avec surprise (et avidité) que vous gagnez très majoritairement – à vue de nez, dans environ 3 cas sur 4. Puisque nous avons fait un grand nombre de simulations, la loi des grands nombres nous permet de penser que votre probabilité de gagner est de 3/4, donc bien supérieure à une chance sur deux !

Simulations de tous les choix possibles de l’adversaire

Vous allez peut-être me dire que si mon adversaire avait choisit une autre séquence que FFP, alors il aurait peut-être pu gagner. Nous allons donc simuler les 8 cas de figure possibles, correspondant aux huit séquences que votre adversaire peut choisir au départ: FFF, FFP, FPF, FPP, PFF, PFP, PPF, PPP. Et pour chaque choix de votre adversaire, j’ai mis un choix très précis de séquence qui vous fera gagner…

Voici les simulations (cette fois-ci, j’ai mis les fréquences de victoires, plutôt que les effectifs). Chaque diagramme correspond à une simulation de 10 000 parties:

Vous voyez donc que, quelque soit le choix de séquence de votre adversaire, il existe une séquence qui peut vous faire gagner plus souvent en moyenne !

La stratégie gagnante

Voici la stratégie à suivre pour gagner à ce jeu (avec au passage un très joli moyen mnémotechnique):

Attendez que votre adversaire choisisse d’abord une séquence. C’est important car votre choix optimal dépendra du choix de l’adversaire.
Si votre adversaire choisit la séquence A-B-C (où A, B et C sont Pile ou Face), choisissez la séquence (non B)-A-B où non B est la face opposée de la face B.

Par exemple, si votre adversaire choisit la séquence PFP, choisissez la séquence (non F)PF c’est-à-dire PPF.

Si vous choisissez votre séquence exactement comme indiqué, alors vous êtes assuré d’avoir une probabilité de gain supérieure à celle de votre adversaire. Voici plus précisément le tableau des probabilités:Comme vous le voyez, votre probabilité de gagner peut aller de 2 chances sur 3 jusqu’à 7 chances sur 8 si votre adversaire a le malheur de choisir une séquence peu gagnante comme FFF… Il nous reste maintenant à comprendre pourquoi certaines séquences battent d’autres séquences et voir comment on peut calculer ces probabilités.

Analyse de deux cas

Nous allons étudier deux exemples: un premier cas dans lequel nous ne ferons aucun calcul mais qui nous servira à comprendre pourquoi une séquence peut l’emporter sur l’autre; et un deuxième cas où nous verrons comment on peut calculer les probabilités de gagner que nous avons données plus haut.

Exemple 1: Votre adversaire choisit FFF et vous choisissez PFF

Commençons par une remarque évidente: pour que votre adversaire gagne, il faut qu’à un moment de la partie Face soit tiré (F) puis que Face soit encore tiré juste après (FF) et enfin que Face soit encore tiré (FFF). A contrario, pour que vous gagniez, il faut qu’à un moment de la partie, Pile soit tiré (P) puis que ce soit Face qui sorte (PF) et enfin que Face soit encore tiré juste après (PFF). Une façon très commode de représenter cela est d’utiliser ce qu’on appelle un graphe d’une chaine de Markov: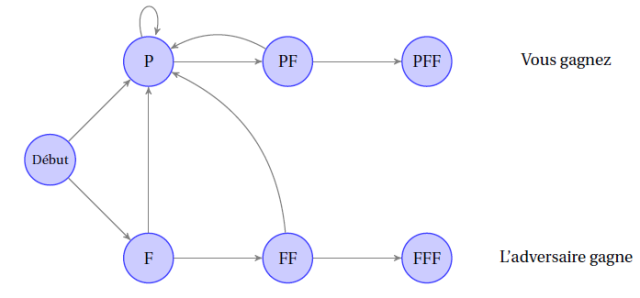Ici, chaque flèche représente un lancer. En fonction de l’endroit où pointe la flèche, on devine si ce lancer était Pile ou Face.

Ce graphe montre clairement l’asymétrie des séquences. On remarque en particulier qu’à partir du moment où un seul Pile est sorti, on sort définitivement de la branche du bas et donc votre adversaire n’a plus aucune chance de gagner. C’est bien cela qui donne un net avantage à la séquence PFF par rapport à la séquence FFF.

Exemple 2: Votre adversaire choisit PFF et vous choisissez PPF

Là encore, on peut tracer le graphe de Markov associé à cette situation:

Nous voyons qu’une fois la séquence ’Pile-Pile’ sortie, votre adversaire n’a plus aucune chance de gagner, ce qui vous donne une plus grande probabilité de gain. Mais de combien exactement est cette probabilité ? C’est ce que nous allons calculer. Pour cela, nous allons d’abord compléter le graphe précédent:

Ce graphe doit se lire de votre point de vue (et non celui de votre adversaire): le but est d’arriver au nœud PPF. A côté de chaque nœud, on a placé une lettre (p, x, y) ou un nombre (1, 0). Cela correspond à la probabilité d’arriver au nœud PPF sachant qu’on part de ce nœud.

Par exemple, la probabilité de partir du nœud Début et d’arriver au nœud PPF est de p (c’est donc la probabilité que vous gagniez la partie !). Autre exemple, imaginons qu’à un moment de la partie, la séquence PF soit sortie: la probabilité que vous gagniez la partie sachant que cette séquence PF vient d’être tirée est notée y. (Bon, au final, y ne nous servira pas dans cet article mais il devait nous servir pour vous montrer une deuxième méthode de calcul de cette probabilité. Mais comme l’article commence à devenir trop long…)

Vous remarquez qu’à côté du nœud PPF nous avons mis 1, car une fois cette séquence sortie, vous êtes sûr d’avoir gagné la partie puisque vous avez gagné la partie ! (J’écris des choses très connes sur ce blog des fois…). Je pense que vous avez maintenant compris pourquoi il y a 0 à côté du nœud PFF…

Passons maintenant au calcul de votre probabilité de gagner la partie, c’est-à-dire au calcul de p. On va utiliser les mêmes règles que pour les arbres de probabilités (dont vous avez sans doute plus l’habitude).

Tout d’abord, il est clair que p=x car, comme on le voit sur le graphe, la partie commence réellement à partir du moment où on a rejoint le noeud P.

Pour calculer x, la formule des probabilités totales nous dit qu’il faut faire la somme des probabilités de tous les chemins qui vont de P à PPF. Et comme pour les arbres de probabilités, la probabilité d’un de ces chemins est le produit des probabilités de transition (qui sont toutes de $\frac{1}{2}$ ici).

Un chemin allant de P à PPF se décompose (dans l’ordre) en:

Un certain nombre de fois n le cycle P-PF, qui a pour probabilité $(\frac{1}{2} \times \frac{1}{2})^n = \frac{1}{4^n}$ .
Une fois le chemin P-PP, qui a pour probabilité $\frac{1}{2}$ .
Un certain nombre de fois m la boucle PP-PP, qui a pour probabilité $\frac{1}{2^m}$
Une fois le chemin final PP-PPF (que j’appelle personnellement le chemin de la gloire) qui a pour probabilité $\frac{1}{2}$ .

Un tel chemin a donc pour probabilité:

$\displaystyle \dfrac{1}{4^n} \times \dfrac{1}{2} \times \dfrac{1}{2^m} \times \dfrac{1}{2} = \dfrac{1}{4} \times \dfrac{1}{4^n} \times \dfrac{1}{2^m}$

Au final, pour trouver x (et donc p), il faut faire la somme des toutes ces probabilités (c’est bien la formule des probabilités totales !):

$\displaystyle p = x = \sum_{n \geq 0, m\geq 0} \dfrac{1}{4} \times \dfrac{1}{4^n} \times \dfrac{1}{2^m} = \dfrac{1}{4} \sum_{n \geq 0} \dfrac{1}{4^n}\sum_{m \geq 0} \dfrac{1}{2^n}$

On reconnaît de gentilles séries géométriques qu’on sait facilement calculer. On a donc

$p = \dfrac{1}{4} \times \dfrac{4}{3} \times 2 = \dfrac{2}{3}$

Nous retrouvons ainsi un résultat que nous avions vu dans le tableau des probabilités plus haut: si votre adversaire joue PFF et que vous jouez PPF alors vous avez 2 chances sur 3 de gagner.

Une variante pour jouer en pratique

Nous l’avons vu, quelque soit le choix de votre adversaire, vous disposez d’un choix de séquence qui vous donne une probabilité plus grande de gagner. Mais cela reste une probabilité et si vous ne jouez qu’une partie, votre adversaire peut toujours gagner.

Afin d’optimiser vos gains, il serait bien de jouer plusieurs parties de suite et de s’appuyer sur la loi des grands nombres (qui dit que votre fréquence de gain tend à se rapprocher de votre probabilité de gagner… songez aux simulations de 10 000 parties qu’on a vues plus haut). Donc, le plus de parties vous ferez, le mieux ce sera pour vous !

Cependant, en pratique, lancer une pièce de monnaie des dizaines de fois de suite peut se révéler fastidieux… Alors pourquoi ne pas utiliser des cartes à jouer au lieu d’une pièce ? C’est ce qu’ont imaginé deux mathématiciens, Yutaka Nishiyama et Steve Humble.

Prenez donc un paquet de 52 cartes. Chaque joueur choisit une séquence, non pas de Pile ou Face, mais de Rouge ou Noir (les couleurs des cartes !). Retournez chaque carte une à une jusqu’à ce qu’une séquence apparaisse. Et tant qu’il reste des cartes dans le paquet, continuez de les retourner !

Cette variante avec des cartes permet de jouer en moyenne environ 7 parties avant d’avoir épuisé toutes les cartes, ce qui, comme on l’a dit plus haut, est avantageux pour le joueur qui a choisi une séquence qui possède une plus grande probabilité de gagner. Mais il y a mieux: cette variante n’étant pas exactement identique à un lancer de pièce (car par exemple, à un moment donné du jeu, il peut rester dans le paquet plus de cartes Rouges que de cartes Noires ou inversement), on peut montrer en fait que les probabilités de gain sont plus grandes que celles obtenues pour le jeu avec des pièces ! (voir référence à la fin de l’article).

Si tu veux devenir riche, commence donc par prendre un paquet de cartes !

Références:

Le jeu qui consiste à lancer la pièce plusieurs fois s’appelle le jeu de Penney.
L’article de Nishiyama et Humble sur l’utilisation d’un jeu de cartes pour jouer: Pattern Matching Probabilities and Paradoxes as a New Variation on Penney’s Coin Game, International Journal of Pure and Applied Mathematics, Vol.59, No.3, 2010, 357-366. (avec au passage un algorithme due au génial Conway!)

13 commentaires pour Arnaquez vos amis à Pile ou Face

Anonyme dit :

23 février 2015 à 22 h 09 min

J’adore ce type de résultat contre intuitif qui montre la force que l’on a de devoir raisonner avec rigueur.

P.S.: il serait bien de fournir les codes utilisés pour les simulations.

J’aimeJ’aime

Réponse

blogdemaths dit :

3 mars 2015 à 20 h 19 min

Je n’ai pas mis le code car, en soi, il n’est pas très intéressant, mais je ferais n’importe quoi pour satisfaire mes lecteurs 😀 Le voici (en langage Python)

import random

joueur1, joueur2 ="FFP", "PFF"
compteur_joueur1, compteur_joueur2 = 0,0

repetitions=10000
for n in range(repetitions):
    suite=""

    for k in range(3):
        piece=random.randint(0,1)
        if piece==0:
            suite += "P"
        else:
            suite += "F"

    while((not suite==joueur1) and (not suite==joueur2)):
        piece=random.randint(0,1)

        if piece==0:
            suite= suite[1]+suite[2]+ "P"
            
        else:
            suite= suite[1]+suite[2]+ "F"

    if suite==joueur1:
        compteur_joueur1+=1
    else:
        compteur_joueur2+=1

print("Nombre de parties effectuées: ", repetitions)
print("La suite "+joueur1+" a gagné",compteur_joueur1,"fois")
print("La suite "+joueur2+" a gagné",compteur_joueur2,"fois")

Anonyme dit :

24 mars 2015 à 19 h 38 min

Merci.

Même un code basique éclaire une notion.

J’aimeJ’aime

Réponse

Ping : L’arnaque | L'Endormitoire
Roland Dassonval dit :

27 février 2015 à 20 h 26 min

Merci pour ce billet.
Une animation pour admettre plus facilement ces probabilités d’abord paradoxales:
http://rdassonval.free.fr/flash/pileouface.swf

J’aimeJ’aime

Réponse
The Dude dit :

24 mars 2015 à 16 h 52 min

Superbe article ! Merci !

J’aimeJ’aime

Réponse
Muriel dit :

6 novembre 2015 à 6 h 46 min

Votre truc est absolument dégueulasse, ça ne marche pas pas du tout, ça pue le caca donc allez vous faire mettre conard de chienne de Redoute

J’aimeJ’aime

Réponse
Kaina dit :

20 Mai 2018 à 17 h 15 min

Superbe article 😉
Pourriez vous me dire svp avec quel logiciel avez vous fais les graphes?

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  21 Mai 2018 à 9 h 46 min
  
  Merci ! Les graphes ont été faits en Latex avec le package Tikz.
  
  J’aimeJ’aime
  
  Réponse
  - Kaina dit :
    
    22 Mai 2018 à 12 h 41 min
    
    merci 🙂
    
    J’aimeJ’aime
    
    Réponse
Anonyme dit :

3 juillet 2018 à 14 h 43 min

bonjour,

les calculs réalisés, si je ne me trompe pas, supposent qu’après chaque fois qu’une séquence perdante ou gagnante est sortie, on reparte au début (pas de séquence glissante).

J’aimeJ’aime

Réponse
Pasquier dit :

21 novembre 2018 à 0 h 13 min

C’est très bien présenté et très intéressant. Bravo.
Ne connaissant pas la syntaxe de Python, j’ai du mal à transformer votre programme en javascript.
êtes-vous en mesure de le faire? Merci

J’aimeJ’aime

Réponse
Pasquier dit :

18 avril 2020 à 19 h 18 min

C’est encore moi. J’ai finalement fais le programme en javascript sans m’inspirer de celui qui précède. Rien de compliqué. Je voulais simplement comparer les techniques.

J’aimeJ’aime

Réponse

Laisser un commentaire Annuler la réponse.

Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur la façon dont les données de vos commentaires sont traitées.