2015, année palindromique

Une nouvelle année commence, et qui dit nouvelle année, dit nouvelles propriétés ! Étonnamment, les articles que j’avais écrit en 2013 et 2014 sont encore valables pour 2015. Mais j’ai pris la résolution d’arrêter d’être fainéant cette année, et voici donc un autre article, spécialement consacré à 2015.

Bob

Vous connaissez le rapport entre le groupe ABBA et le XANAX ? Non, la réponse n’est pas qu’il faut être drogué pour pouvoir apprécier un groupe de musique suédois (quoi que…). Le lien entre les deux est que ces deux termes sont ce qu’on appelle des palindromes, c’est-à-dire des mots qui se lisent de droite à gauche ou de gauche à droite de la même façon.

En mathématiques, la notion de nombre palindrome est similaire: ce sont les nombres qui, quand ils sont lus dans un sens ou dans l’autre, ne changent pas. Par exemple, 121 et 9009 sont des palindromes.

Quel est le lien avec 2015 dans tout ça ? Car il est clair que ce n’est pas un palindrome. Mais quelque part dans l’horloge de votre ordinateur, le nombre 2015 est stocké sous forme d’un nombre binaire (avec des 0 et des 1). Et l’écriture de 2015 en binaire est:

11111011111

qui lui est un palindrome ! Je vous propose dans cet article de voir s’il y a eu (et s’il y aura) beaucoup d’années qui sont des palindromes en binaire, ce qui sera un prétexte pour faire un peu (beaucoup) de dénombrement.

Compter les palindromes à 11 et 12 chiffres

Pour savoir s’il y eu beaucoup d’années palindromes en binaire avant 2015 (et plus généralement, la proportion de nombres qui sont des palindromes en binaire), nous allons commencer par dénombrer tous les palindromes binaires à $n$ chiffres, où $n$ est un entier quelconque. Par exemple, 2015 possède 11 chiffres en binaire; commençons donc par trouver combien il y a de palindromes en binaire à 11 chiffres.

Si un nombre possède 11 chiffres exactement, le 1er chiffre est forcément 1 (il ne peut valoir 0, sinon il serait considéré comme un nombre à 10 chiffres !). Et puisque c’est un palindrome, le dernier chiffre sera aussi un 1. Un palindrome à 11 chiffres est donc de la forme: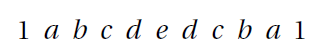Vous voyez qu’on peut choisir librement les 2ème, 3ème, 4ème et 5ème chiffres (représentés par les lettres $a, b, c$ et $d$ ). Puisque il y a 2 possibilités pour chacun de ces chiffres (0 ou 1 !), cela donne $2^4$ possibilités. Une fois choisis, on n’aura pas le choix pour les 10ème, 9ème, 8ème et 7ème chiffres puisqu’il faut qu’il y ait symétrie ! Il reste le chiffre du milieu, qu’on peut choisir librement, ce qui donne deux possibilités supplémentaires.Ainsi, il y a $2^4 \times 2 = 32$ nombres de 11 chiffres en binaire qui sont des palindromes.

Et pour les nombres à 12 chiffres ? Comme 12 est pair, il n’y aura pas de chiffre isolé au milieu; comment fait-on alors ? En fait, pour un nombre à 12 chiffres en binaire, le raisonnement est quasiment le même. Un palindrome à 12 chiffres est de la forme:On peut choisir librement les 2ème, 3ème, 4ème, 5ème et 6ème chiffres, ce qui donne $2^5=32$ possibilités. A partir de là, il n’y a plus guère de choix possible pour les 7ème, 8ème, 9ème, 10ème, 11ème chiffres car ils doivent être respectivement les mêmes que les 6ème, 5ème, 4ème, 3ème et 2ème chiffres.Au final, cela fait 32 nombres à 12 chiffres en binaire qui sont des palindromes.

On voit au passage qu’il y a autant de palindromes à 11 chiffres que de palindromes à 12 chiffres en binaire !

Compter les palindromes dans le cas général

On va compter le nombre d’entiers à $n>0$ chiffres en binaire qui sont des palindromes. Comme dans l’exemple précédent, on distingue deux cas:

1) $n$ est un nombre pair: Dans ce cas, un nombre en binaire à $n$ chiffres se compose de $\frac{n}{2}$ premiers chiffres et de $\frac{n}{2}$ derniers chiffres. Ces derniers étant entièrement déterminés par les $\frac{n}{2}$ premiers. On sait que le premier chiffre est un 1. Il reste donc à choisir $\frac{n}{2} - 1$ chiffres ce qui donne $2^{\frac{n}{2} - 1}$ possibilités.

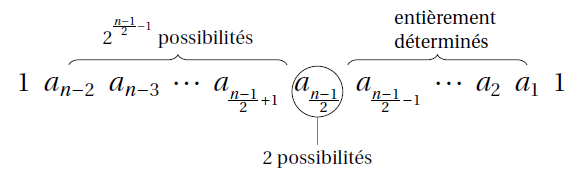
2) $n$ est un nombre impair: Dans ce cas, il y a $\frac{n-1}{2}$ premiers chiffres, puis un chiffre du milieu puis $\frac{n-1}{2}$ derniers chiffres. Comme toujours, le premier chiffre est un 1. Ensuite, on peut choisir librement les $\frac{n-1}{2} - 1$ chiffres suivants, ainsi que le chiffre du milieu.

Cela donne $2^{ \frac{n-1}{2} - 1} \times 2 = 2^{\frac{n-1}{2}}$ possibilités.

Résumons: si on note $P(n)$ le nombre d’entiers à $n$ chiffres en binaire qui sont des palindromes (en binaire) alors:

$P(n) = \begin{cases} 2^{\frac{n}{2}} & \text{si n pair} \\ 2^{\frac{n-1}{2}} & \text{si n impair} \end{cases}$

Nombre de palindromes

En incluant 2015, il y a eu 93 années depuis l’an 1 qui sont des palindromes en binaire. Les voici:

1, 3, 5, 7, 9, 15, 17, 21, 27, 31, 33, 45, 51, 63, 65, 73, 85, 93, 99, 107, 119, 127, 129, 153, 165, 189, 195, 219, 231, 255, 257, 273, 297, 313, 325, 341, 365, 381, 387, 403, 427, 443, 455, 471, 495, 511, 513, 561, 585, 633, 645, 693, 717, 765, 771, 819, 843, 891, 903, 951, 975, 1023, 1025, 1057, 1105, 1137, 1161, 1193, 1241, 1273, 1285, 1317, 1365, 1397, 1421, 1453, 1501, 1533, 1539, 1571, 1619, 1651, 1675, 1707, 1755, 1787, 1799, 1831, 1879, 1911, 1935, 1967, 2015

Pour les trouver, j’ai écrit un petit programme mais il serait plus intéressant d’avoir une formule qui donne le nombre de palindromes qu’il y a eu avant telle ou telle année…. malheureusement, une telle formule n’est pas forcément facile à déterminer. On va donc s’en passer et nous allons plutôt essayer de trouver une estimation du nombre de palindrome inférieurs à un nombre donné.

Si $x$ un entier (qui représente donc une année), on note $N(x)$ le nombre d’entiers positifs non nuls qui sont inférieurs ou égaux à $x$ et qui sont des palindromes en binaire. Par exemple, on vient de voir que $N(2015)=93$ car il y eu 93 années avant 2015 qui étaient des palindromes en binaire. Voici le graphe de la fonction $N(x)$ pour $x$ compris entre 1 et 2015:

Vu la gueule du graphe, vous comprenez mieux pourquoi on ne va pas chercher une formule exacte pour N(x) !

Comme j’ai dit, notre but sera d’essayer d’estimer $N(x)$ pour voir si, à l’avenir, il y aura beaucoup d’années qui sont des palindromes en binaires.

Certes, trouver une formule pour $N(x)$ n’est pas chose aisée, mais il y a quand même des cas simples où il existe une formule exacte: par exemple dans le cas où $x$ est de la forme $2^{n}$ . En effet, $2^{n}$ est le plus petit nombre à $n$ chiffres en binaire et n’est pas un palindrome donc, pour trouver $N(2^n)$ , il suffit d’additionner le nombre de palindromes à $n-1$ chiffres avec le nombre de palindromes à $n-2$ chiffres avec le nombres de palindromes à $n-3$ chiffres, etc. Mais nous avons déjà vu combien il y a de palindromes à $k$ chiffres ! Je ne mets pas les calculs, mais voici la formule (vous pourrez trouver la démonstration de cela à la fin de l’article):

$N(2^n) = \begin{cases} 2 (2^{\frac{n}{2}} - 1) & \text{si } n \text{ est pair} \\ 3 \times 2^{\frac{n-1}{2}} - 2 & \text{si } n \text{ est impair} \end{cases}$

Passons à l’estimation de $N(x)$ pour $x$ un entier quelconque. Puisque tout entier peut être encadré par deux puissances de 2 successives, il existe un entier $n$ tel que

$2^n \leq x < 2^{n+1}$

Et comme la fonction $N$ est croissante (le nombre de palindromes ne peut diminuer au fur et à mesure des années !), on a

$N(2^n) \leq N(x) \leq N(2^{n+1})$

Selon que $n$ est pair ou impair, on a donc soit:

$2(2^{\frac{n}{2}}-1) \leq N(x) \leq 3 \times 2^{\frac{n}{2}} - 2$

soit

$3 \times 2^{\frac{n-1}{2}} - 2 \leq N(x) \leq 2(2^{\frac{n+1}{2}}-1)$

Ainsi la proportion d’années qui sont des palindromes en base 2, à savoir $\frac{N(x)}{x}$ est encadrée par

$\dfrac{2(2^{\frac{n}{2}}-1)}{2^{n+1}} \leq \dfrac{N(x)}{x} \leq \dfrac{3 \times 2^{\frac{n}{2}} - 2}{2^n}$

ou par

$\dfrac{3 \times 2^{\frac{n-1}{2}} - 2}{2^{n+1}} \leq \dfrac{N(x)}{x} \leq \dfrac{2(2^{\frac{n+1}{2}}-1)}{2^n}$

Conclusion

A partir de là, on voit que les suites qui encadrent $\frac{N(x)}{x}$ tendent vers 0 quand $n$ tend vers l’infini (plus précisément, si $x$ possède $n$ chiffres en binaire alors $N(x)/x$ est de l’ordre de $2^{-\frac{n}{2}}$ ), ce qui signifie que plus $x$ est grand, et plus le nombre de palindromes en binaire tend à se raréfier ! Cela se voit très bien sur le graphique suivant:

Donc, même si vous n’avez pas compris tous les calculs, ce qu’il faut retenir est qu’il y a peu d’années qui sont des palindromes en binaire et donc 2015 est une année remarquable !

Mais ce n’est pas tout ! Il y a mieux !

Nous avons vu que 2015 est un palindrome en base 2. C’est aussi un palindrome en base 38, 64, 154, 402 et 2014. Une curiosité supplémentaire est la suivante: la décomposition en produits de facteurs premiers de 2015 est

2015 = 13 x 5 x 31

Et vous reconnaissez une sorte de palindrome ! Amusant, non ? Cela vient du fait que 13 et 31 sont ce qu’on appelle des Reimerp c’est-à-dire que ce sont des nombres premiers qui sont encore premiers quand on les « renverse ». D’autres exemples sont 37 et 73 ou bien 113 et 311.

Bref, ça fait beaucoup de belles choses pour un simple nombre. Bonne année 2015 à tous !

Note:

Voici la démonstration pour la formule de $N(2^n)$ :

Calcul de $N(2^n)$

4 commentaires pour 2015, année palindromique

Adou Ondongo Arnold dit :

4 janvier 2015 à 13 h 10 min

Bonjour , Juste pour vous dire que j’apprécie énormément vos articles et pour vous souhaiter une bonne année 2015 . Merci et bravo pour votre travail !

Arnold ADOU ONDONGO

Fax : [caché]

>

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  4 janvier 2015 à 18 h 05 min
  
  Merci Arnold et bonne année !
  
  J’aimeJ’aime
  
  Réponse
Céline dit :

5 janvier 2015 à 13 h 20 min

Tout d’abord bonne année à vous, je vous souhaite beaucoup d’inspiration.
Ensuite une question : pour la détermination du nombre de palindromes binaires à $n$ chiffres lorsque $n$ est pair, vous trouvez $P(n)=2^{\frac{n-1}{2}}$ et je suis d’accord avec votre démonstration. Mais dans votre résumé vous écrivez $P(n)=2^{\frac{n}{2}}$, et vous reprenez ce résultat pour la démonstration en fin d’article. Est-ce une erreur ou alors y a-t-il quelque chose qui m’échappe ?
Merci, et bravo pour vos articles toujours plaisants à lire.

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  5 janvier 2015 à 16 h 57 min
  
  En effet il y a un petit souci… va falloir que je modifie des choses.
  Merci de votre vigilance et bonne année !
  
  J’aimeJ’aime
  
  Réponse

Répondre à blogdemaths Annuler la réponse.

Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur la façon dont les données de vos commentaires sont traitées.