Dans l’article précédent, nous avons vu un problème de contact dont le but était de construire un cercle à la fois tangent à une droite et un cercle donnés. Je vous propose un deuxième problème de contact, où, cette fois-ci, le but n’est pas la construction d’un cercle mais le calcul de son rayon.
Le problème que je vais vous proposer ci-dessous est un sangaku. Les sangakus étaient des problèmes géométriques d’origine japonaise, qui étaient gravés sur des tablettes en bois et accrochés dans les temples. Pour en savoir plus, vous pouvez consulter la page Wikipédia à ce sujet.
Le problème ! Le problème !
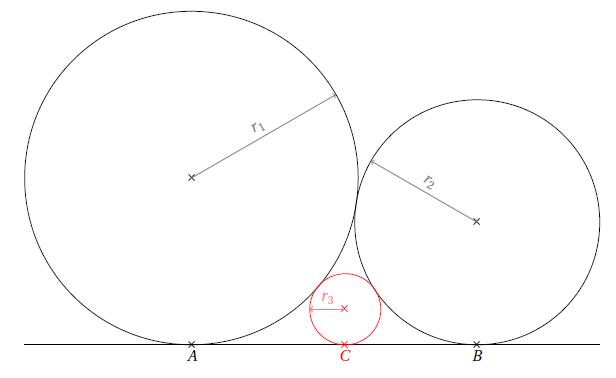
Voici sans plus attendre l’énigme à résoudre avec ce sangaku:
Soit
et
deux cercles tangents, et
une droite tangente à ces deux cercles. On admet qu’il est possible de construire un troisième cercle qui est à la fois tangent aux cercles et à la droite. Question: si on connaît les rayons
et
des deux premiers cercles, que vaut le rayon
du troisième cercle ?
Résolution
La résolution de ce problème utilisera la petite formule que nous avions démontrée dans l’ article précédent (Full contact – Episode I) (que je vous conseille d’aller lire !). Pour rappel, voici ce que nous avions démontré:
Si on revient à notre sangaku, on peut appliquer notre formule trois fois:
sont tangents donc:
D’autre part, comme les points 
On remplace chaque distance par l’expression que nous avons vue ci-dessus:
c’est-à-dire:
Il reste à isoler
Ce ne serait pas une petite identité remarquable, là ? Mais oui !
Et on obtient:
On pourrait s’arrêter là mais on peut mettre cette formule sous une autre forme que je trouve plus élégante. Commençons par prendre l’inverse de l’égalité précédente:
Puis prenons la racine carrée dans les deux membres:
ce qui donne la belle formule:
Cette formule fait penser à la formule obtenue en physique quand on met des résistances en parallèles !
Et la construction alors ?
Il est possible de construire le troisième cercle tangent à la règle et au compas, mais bien que la construction en elle-même ne soit pas trop dure, la justification est un peu plus subtile et je me suis donc bien gardé d’en parler dans cet article. Mais pour les gens intéressés, l’idée de la construction peut être vue ici… (attention, c’est en Anglais !).
Pour finir, des coordonnées
Pour terminer cet article, donnons un reformulation en termes de coordonnées qui peut être utile. On suppose qu’on s’est donné un repère et que la tangente commune aux cercles est l’axe des abscisses:
On suppose que les coordonnées des centres des deux premiers cercles sont connues. Quelles sont les coordonnées du centre du troisième cercle ? Nous voyons tout d’abord que son ordonnée est son rayon 
Ainsi, les coordonnées du troisième cercle tangent sont:
Au final, ce n’était pas un problème si simple que cela, il y avait pas mal de boulot. Ils ne se foutaient pas de la gueule des gens quand ils posaient des sangakus à l’époque !
Note:
Pour l’anecdote, ce sangaku-ci (coup ça) fut posé en 1824 sur une tablette dans les environs de la préfecture de Gunma au centre du Japon (source).
Blogdemaths 
Très bel exposé avec une jolie moyenne harmonique sur des racines carrées comme formule.
J’aimeJ’aime
Merci 🙂
J’aimeJ’aime
C’est effectivement une jolie formule!
PS Ce n’est pas une moyenne harmonique.
J’aimeJ’aime
En effet, c’est une « presque » moyenne harmonique
J’aimeJ’aime
Complément d’anecdote : il s’agit en fait d’un cas limite du célèbre problème des contacts d’Apollonius (bien plus ancien donc que 1824) ou plus précisément du thèorème de Descartes, lorsqu’on fait tendre le rayon d’un des cercles vers l’infini.
J’aimeJ’aime
Merci pour l’anecdote !
J’aimeJ’aime