Produit des diagonales d’un polygone régulier

Prenez un cercle de rayon 1 et inscrivez-y un polygone régulier. A partir d’un des sommets de ce polygone, tracez tous les segments qui le joigne aux autres sommets du polygone (voir figure ci-dessous). Si votre polygone possède $n$ sommets, vous obtenez ainsi $n-1$ segments (qui s’appellent les diagonales du polygone). Faites le produit des longueurs de ces diagonales. Qu’obtenez-vous ?

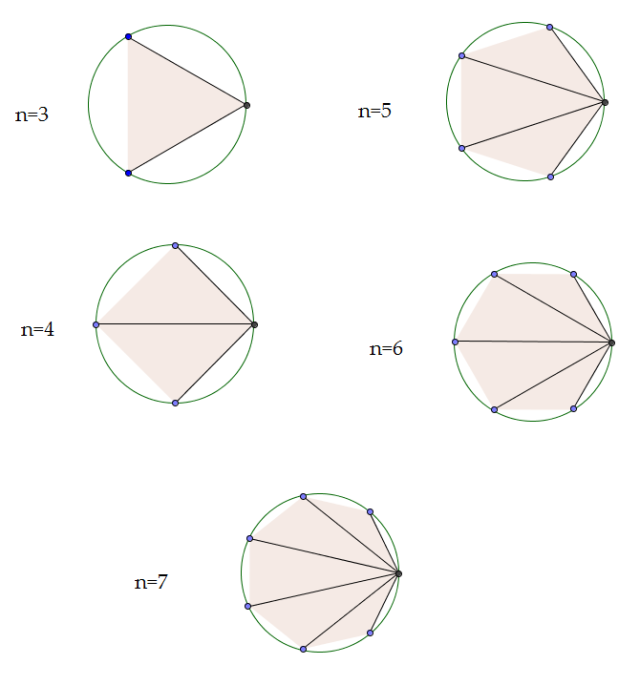
On appelle diagonale d’un polygone tout segment joignant deux sommets. Allons-nous calculer la longueur de toutes ces diagonales afin de faire leur produit ?

Étude du cas n=3

Comme d’habitude, nous allons commencer par étudier ce qui se passe pour des petites valeurs de $n$ et on commence par le cas d’un triangle équilatéral. Il s’agit ici de déterminer la longueur $a$ d’un côté d’un triangle équilatéral qui est inscrit dans un cercle de rayon 1. C’est en soi un petit problème géométrique dont nous allons donner deux solutions.

Méthode n°1: Centre de gravité

On utilise les faits suivants:

Dans un triangle équilatéral de côté $a$ , chaque médiane a pour longueur $a \frac{\sqrt{3}}{2}$ (cela se montre avec Pythagore car une médiane est aussi une hauteur).
Dans un triangle équilatéral les médianes et les médiatrices coïncident donc le centre du cercle circonscrit est aussi le centre de gravité. Et on sait que la distance d’un sommet au centre de gravité est égale à 2/3 de la médiane.

Ainsi, $\frac{2}{3} \times a \frac{\sqrt{3}}{2} = 1$ d’où $a=\frac{3}{\sqrt{3}} = \sqrt{3}$ !

Méthode n°2: Loi des sinus

La loi des sinus nous dit que, dans un triangle, si on a un angle $\alpha$ et si le côté opposé à cet angle a pour longueur $a$ alors $\dfrac{a}{\sin(\alpha)}=2R$ où $R$ est le rayon du cercle circonscrit au triangle. Dans notre cas, cela donne $\dfrac{a}{\sin( \pi /3)} = 2$ car tous les angles d’un triangle équilatéral valent $\pi/3$ et car le rayon du cercle circonscrit est supposé être égal à 1. Comme $\sin( \pi /3) = \dfrac{\sqrt{3}}{2}$ , on en déduit que $a = 2 \times \dfrac{\sqrt{3}}{2} = \sqrt{3}$ .

On peut calculer la longueur d’un côté d’un triangle équilatéral à l’aide de la loi des sinus.

Revenons à présent au produit des diagonales. Puisque chaque diagonale a pour longueur $\sqrt{3}$ , le produit cherché vaut $A_0A_1 \times A_0A_2 = \sqrt{3} \times \sqrt{3} = 3$ . Trois, comme le nombre de sommets (certains diront comme le nombre de mousquetaires ou bien comme le nombre de Bee Gees). Coïncidence ? Suspense.

Étude du cas n=4

Le cas d’un carré inscrit dans un cercle de rayon 1 est plus simple. Il suffit de savoir que la diagonale d’un carré de côté 1 vaut $\sqrt{2}$ :

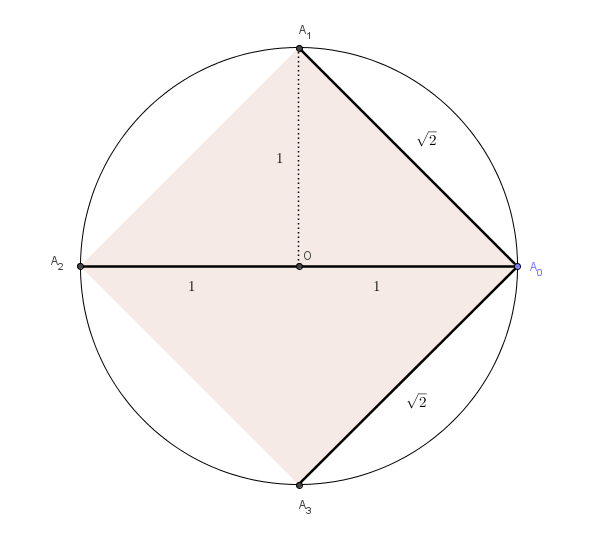Le produit des diagonales vaut donc $A_0 A_1 \times A_0 A_2 \times A_0 A_3 = \sqrt{2} \times 2 \times \sqrt{2}=4$ . Donc, pour quatre sommets, le produit vaut 4. Amazing !

Vous prendrez bien un peu d’algèbre avec vos polygones ?

Nous allons donc prouver que, dans le cas général d’un polygone régulier à $n$ côtés, le produit des diagonales issues d’un sommet vaut $n$ . Et nous allons faire cela de manière purement algébrique. Quoi ? Oui, vous entendez bien. Autant nous avons montré cette propriété géométriquement dans le cas $n=3$ et $n=4$ , autant là, pour généraliser et prouver cela facilement, on va utiliser le formalisme des polynômes et l’élégance des nombres complexes.

Commençons par rappeler que les sommets d’un polygones régulier inscrit dans un cercle de rayon 1 peuvent être vus comme des nombres complexes: les $n$ sommets sont représentés par les nombres $1, \text{e}^{\frac{i 2\pi}{n}}, \cdots, \text{e}^{k \frac{i 2\pi}{n}}, \cdots, \text{e}^{(n-1) \frac{i 2\pi}{n}}$ .

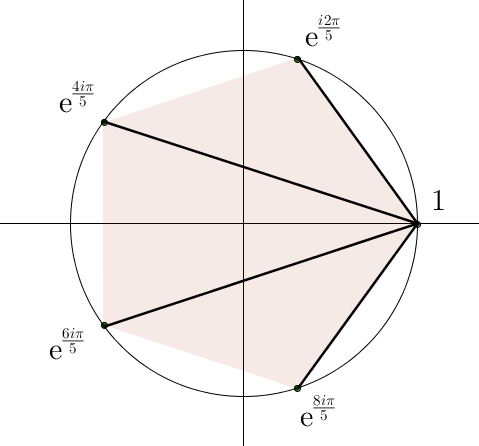
Chaque sommet peut être représenté à l’aide de nombres complexes. La longueur d’une diagonale s’exprime alors comme le module de la différence des affixes.

De plus, chaque diagonale a pour longueur $OA_k = |1 - \text{e}^{k \frac{i 2 \pi}{n}}|$ . Ainsi, le produit des diagonales est égal à $| (1-\text{e}^{ \frac{i 2\pi}{n}} - 1) (1-\text{e}^{2 \frac{i 2\pi}{n}} ) \cdots (1-\text{e}^{(n-1) \frac{i 2\pi}{n}} )|$ . Nous allons calculer ce produit très astucieusement, sans faire véritablement de calcul.

Rappelons auparavant que les nombres $\text{e}^{k \frac{i 2\pi}{n}}$ (pour $k$ allant de 1 à n-1) sont racines du polynôme:

$X^n -1= (X-1)(1 + X + X^2 + \cdots + X^{n-1})$

Comme ils n’annulent pas le polynôme $X-1$ , ils sont donc racines du polynôme $1+ X + X^2 + \cdots + X^{n-1}$ que nous pouvons donc factoriser de la façon suivante:

$1+ X + X^2 + \cdots + X^{n-1} = (X - \text{e}^{ \frac{i 2\pi}{n}} ) \cdots (X- \text{e}^{(n-1) \frac{i 2\pi}{n}})$

Maintenant (astuce géniale !), si on remplace $X$ par $1-X$ dans cette égalité, on trouve:

$1+ (1-X) + (1-X)^2 + \cdots + (1-X)^{n-1} = (1- X - \text{e}^{ \frac{i 2\pi}{n}} ) \cdots (1 - X- \text{e}^{(n-1) \frac{i 2\pi}{n}})$

ce qui donne

$1+ (1-X) + (1-X)^2 + \cdots + (1-X)^{n-1}= ((1 - \text{e}^{ \frac{i 2\pi}{n}}) - X ) \cdots ((1 - \text{e}^{(n-1) \frac{i 2\pi}{n}}) - X)$

Nous disposons donc de deux polynômes qui sont égaux. On va développer (enfin pas entièrement) chacun d’entre eux et utiliser le fait que les termes constants doivent être égaux.

1) On sait d’après la formule du binôme de Newton que $(1-X)^k = 1 + {k \choose 1}(-X) + {k \choose 2}(-X)^2 + \cdots + {k \choose k}(-X)^k$ donc le terme constant de ce polynôme est 1. Par suite, le terme constant du polynôme

$1+ (1-X) + (1-X)^2 + \cdots (1-X)^{n-1}$

est $1 + 1 + \cdots + 1 = n$ .

2) Si on note $w_k =1 - \text{e}^{k \frac{i 2\pi}{n}}$ alors on a:

$((1 - \text{e}^{ \frac{i 2\pi}{n}}) - X ) \cdots ((1 - \text{e}^{(n-1) \frac{i 2\pi}{n}}) - X) = (w_1 - X) \cdots (w_{n-1} -X)$

Et quand on développe le membre de droite, le terme constant est $w_1 \times w_2 \times \cdots \times w_{n-1}$ .

Comme les termes constants doivent être les mêmes, on en déduit que

$n = w_1 \times w_2 \times \cdots \times w_{n-1}$

c’est-à-dire

$n = (1 - \text{e}^{ \frac{i 2\pi}{n}}) \cdots (1 - \text{e}^{ (n-1)\frac{i 2\pi}{n}})$

En prenant le module de cette relation, on en déduit donc que le produit des diagonales est bien égal à $n$ . En un mot: la puissance de l’algèbre (ce qui fait cinq mots en fait).

Une belle identité trigonométrique

En fait, il est possible d’exprimer d’une autre façon les longueurs des diagonales ce qui nous donnera une très jolie relation.

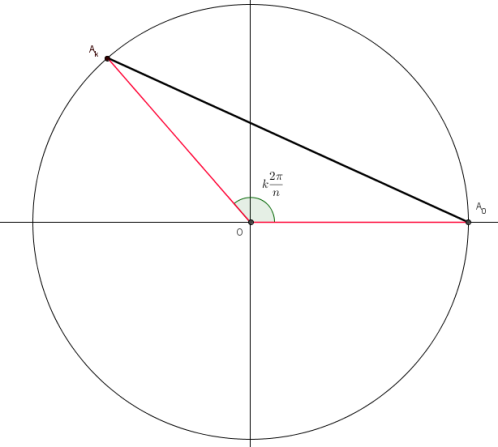
On peut utiliser la loi des sinus pour exprimer la distance $A_0A_k$ . Tout d’abord, on sait que l’angle au centre $A_0OA_k$ vaut $\frac{2 \pi}{n}$ (car on est en présence d’un polygone régulier):

On introduit ensuite un point $M$ quelconque sur le cercle. D’après le théorème de l’angle au centre, l’angle $\alpha$ de la figure ci-dessous vaut la moitié de l’angle $A_0OA_k$ , c’est-à-dire $\frac{k \pi}{n}$ :

Enfin, puisque le triangle $A_0MA_k$ est inscrit dans le cercle de rayon 1, d’après la loi des sinus, on a $\dfrac{A_0A_k}{\sin(k \pi / n)} = 2 \times 1$ , d’où:

$A_0A_k = 2 \sin(\frac{k \pi}{n})$

Mais comme on a vu que $A_0 A_1 \times A_0A_2 \times \cdots \times A_0 A_{n-1} =n$ , on en déduit que

$2 \sin(\frac{\pi}{n}) \times 2 \sin(\frac{2 \pi}{n}) \times \cdots \times 2 \sin(\frac{(n-1) \pi}{n}) =n$

Nous venons donc de démontrer dans cet article, presque sans faire aucun calcul, que:

$\boxed{ \prod_{k=1}^{n-1} \sin\left( \frac{k \pi}{n}\right) = \frac{n}{2^{n-1}}}$

Référence:

La très jolie démonstration du fait que le produit des diagonales vaut $n$ que nous avons reproduit dans cet article est due à un certain Barry Lewis (dans un article intitulé Power chords).

10 commentaires pour Produit des diagonales d’un polygone régulier

Pierre Lecomte dit :

2 décembre 2013 à 12 h 45 min

C’est très joli!

PS Pour égaler les termes constants, pas besoin de développer ne fut-ce qu’un peu. Il suffit d’évaluer les deux polynômes en 0.

J’aimeJ’aime

Réponse
- Pierre Lecomte dit :
  
  2 décembre 2013 à 12 h 46 min
  
  Zut! J’ai, fait une faute d’orthographe! Désolé!
  
  J’aimeJ’aime
  
  Réponse
- blogdemaths dit :
  
  2 décembre 2013 à 13 h 19 min
  
  Bonne idée ! Je n’y avais pas pensé, merci de l’astuce Pierre.
  Ca fait encore moins de calcul comme ça 🙂
  
  J’aimeJ’aime
  
  Réponse
The Dude dit :

4 décembre 2013 à 4 h 43 min

Excellent article ! Je me rappelle la première fois que je suis tombé là-dessus. Une question laissée sur Twitter qui trouve son chemin dans la mer de gazouillis… J’étais estomaqué par le résultat !

J’avais d’ailleurs commencé à écrire un billet sur le sujet mais par paresse il est resté dans mes brouillons trop longtemps.

Je ne sais pas si vous connaissiez, mais la « version un peu plus forte » du résultat est le théorème de Cotes, qu’on peut trouver ici sur wiki : http://goo.gl/775zR5

Du point de vue historique, c’est aussi intéressant (attention : pas mal de name dropping dans le prochain paragraphe…)

Apparament, Roger Cotes est tombé sur son théorème en réfléchissant à une conjecture (fausse) de Liebniz, énoncée en 1702 dans son livre Acta Eruditorum, à propos d’intégrales qui peuvent s’exprimer ou non avec des fonctions logarithmiques et trigonométriques (plus spécifiquement, des intégrales de la forme int(dx/(x^n + a^n) où n est une puissance de 2). Cotes a répondu à Liebniz, mais n’a pas fourni la preuve à sa méthode permettant de factoriser l’expression x^n + a^n. Le premier à fournir la preuve du théorème est Henri Pemberton, l’éditeur de la troisième version de Principia de Newton, en 1722. Johann Bernoulli a dit que la preuve de Pemberton était « longue, fastidieuse et intriquée ». Évidemment, Pemberton n’utilisait pas les nombres complexes.

C’est grâce au physicien Robert Smith (1689-1768), le cousin de Cotes, qui inclut le théorème dans son Harmonia Mensurarum (après avoir reconstruit la démarche empruntée par Cotes, grâce à ses manuscrits laissés après sa mort soudaine) qu’on peut aujourd’hui connaître le début de l’histoire de cet étonnant résultat.

(Infos prises dans Paul J. Nahin (1998), An imaginary Tale. Nahin offre aussi dans son livre une preuve simple qui tient en quelques lignes)

J’aimeJ’aime

Réponse
- blogdemaths dit :
  
  4 décembre 2013 à 19 h 41 min
  
  Merci de ces très intéressantes précisions historiques que je ne connaissais pas ! Tout comme je ne connaissais pas le théorème de Cotes. Tout ça est très beau 🙂
  
  J’aimeJ’aime
  
  Réponse
Roland Dassonval dit :

8 janvier 2014 à 13 h 57 min

Bonjour,
Merci pour cet article.
J’ai repris l’idée qui pourrait attiser la curiosité de quelques élèves à partir de la troisième, une occasion de revoir un peu de trigonométrie, de faire des calculs avec radicaux…
http://rdassonval.free.fr/flash/cordes.swf
Roland Dassonval.

J’aimeJ’aime

Réponse
Julian Favennec dit :

27 juin 2014 à 15 h 06 min

merci de démontrer ce résultat que j’avais déjà trouvé par moi même.

J’aimeJ’aime

Réponse
. dit :

1 mars 2015 à 17 h 33 min

Qu’en est-il pour n=6? Ou encore n=12? Et, au final, que vaut le produit des n-1 cordes?

Super article!

J’aimeJ’aime

Réponse
blogdemaths dit :

1 mars 2015 à 21 h 14 min

Merci 🙂

Pour répondre à votre question, si n=6 alors le produit des cordes vaut 6, et si n=12 alors le produit des corde vaut 12….

J’aimeJ’aime

Réponse
Pasquier dit :

18 avril 2020 à 21 h 06 min

En utilisant les expressions des côtés du pentagone régulier convexe et du pentagone régulier étoilé, expressions qui sont respectivement R[racine de (10-2 fois racine de 5)] / 2 et R[racine de (10+2 fois racine de 5)] / 2, on obtient immédiatement le résultat 5 (en faisant R=1) qui est le produit du carré de la première expression par le carré de la seconde.
Cela est exposé dans l’ouvrage de Lebossé Hémery classe de seconde, qu’on utilisait il y a 60 ans.
Tous ces résultats sont bien oubliés aujourd’hui.
On peut aussi trouver le résultat très simplement pour l’octogone régulier sachant que les côtés de l’octogone régulier convexe et étoilé ont respectivement pour valeur R[racine de (2 – racine de 2)] et
R[racine de (2 + racine de 2)]. Je rechigne à écrire le calcul très simple qui en découle. On arrive bien à 8.

J’aimeJ’aime

Réponse