Un tour de magie mathématique…

Ce que je vais vous apprendre dans cet article va changer votre vie. Vous allez passer de simple inconnu banal à star mondiale de la magie. Vous allez faire passer David Copperfield pour un amateur.

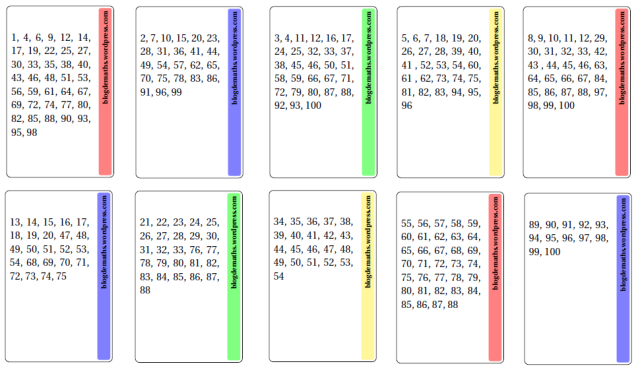
Aller, trêve de publicité mensongère et d’accroche gratuitement racoleuse, je vais vous présenter un petit tour de magie mathématique bien sympathique. La seule chose dont vous aurez besoin, ce sont les 10 cartes suivantes (que j’ai confectionnées moi-même… elles sont pas trop PIMP mes cartes « blogdemaths » ?):

Pour une version imprimable (en pdf), cliquez ici: Cartes magiques. Pour information, ces cartes ont été réalisées (par mes soins) en LaTeX et plus précisément à l’aide du (génialissime) package Tikz.

Mise en œuvre 

Voici comment se déroule le tour:

1. Demandez à un spectateur de choisir un nombre au hasard entre 1 et 100 et de l’inscrire sur une feuille de papier  à l’abri des regards indiscrets.
2. Montrez-lui tour à tour chacune des 10 cartes ci-dessus, et demandez-lui à chaque fois si le nombre qu’il a choisi est inscrit sur la carte.
3. Faites semblant de réfléchir/de regarder dans votre boule de cristal/d’invoquer l’esprit de l’accordéon Yvette Horner… Bref, faites votre magicien.
4. Annoncez-lui le nombre qu’il avait choisi au départ. Demandez-lui de retourner le papier pour confirmer que c’était bien le nombre qu’il avait choisi.
5. Récoltez les fruits de votre nouvelle célébrité.

(Remarque: Le fait d’écrire le nombre sur un papier n’est pas nécessaire mais il y a toujours des enf…. des plaisantins qui changeront de nombre à la fin et diront que ce n’est pas le nombre qu’ils avaient choisi juste pour nous prouver que notre tour ne marche pas… mais on ne blague pas avec les mathématiques. ON NE BLAGUE PAS AVEC LES MATHÉMATIQUES.)

Mais comment marche ce tour ? On est sur blogdemaths, donc vous vous doutez bien qu’il n’y a pas de sorcellerie derrière tout cela, mais seulement des mathématiques.

Un petit exemple…

Imaginons que vous soyez le spectateur et que vous choisissiez le nombre 32. Voyons toutes les cartes qui contiennent le 32:

Voici les 3 seules cartes du jeu qui contiennent le numéro 32

Maintenant, je vous laisse essayer de deviner comment on peut trouver le nombre 32 à partir de ces cartes.

Vous avez trouvé ? Il suffit d’additionner les nombres les plus en haut à gauche.

3+8+21 = 32. Le compte est bon.

Ainsi, chaque fois que la personne vous dit que le nombre qu’elle a choisi est inscrit sur une carte, vous additionnez le nombre qui apparaît en haut à gauche de cette carte. Le total de tous ces nombres vous donnera le nombre choisi par le spectateur.

On ne peut pas faire de tour plus simple à exécuter ! (A condition bien entendu de savoir additionner mentalement quelques nombres…) Et très franchement, très peu de gens s’apercevront qu’on n’a fait qu’une simple somme.

Explication mathématique du tour

L’explication, même si elle est simple a posteriori, est loin d’être évidente et requiert l’utilisation d’un théorème que nous avons déjà démontré dans ce blog: le théorème de Zeckendorf. Rappelons ce que nous dit ce théorème:

Tout entier naturel non nul s’écrit de manière unique comme la somme de nombres de Fibonacci non consécutifs.

Si vous remarquez bien, le premier nombre de chaque carte est un nombre de Fibonacci. Rappelons que la suite de Fibonacci est la suivante: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. Et tout nombre inférieur à 100 peut s’écrire comme une somme de ces nombres, et ce, de manière unique.

Ainsi, chaque nombre entier compris entre 1 et 100 n’apparaît que sur une unique combinaison de cartes. Par exemple, le nombre 32 est l’unique nombre à apparaître à la fois sur les cartes commençant par 3, 8 et 21 et à n’apparaître sur aucune autre carte. On ne peut pas se tromper !

Comment a-t-on réalisé ces cartes ? Très simplement, en commençant par prendre 10 cartes vierges, et en écrivant 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 sur chacune d’entre elle. Puis, pour tout entier inférieur à 100, on a effectué sa décomposition de Zeckendorf, et on a inscrit ce nombre sur chacune des cartes correspondant. Par exemple, puisque la décomposition de 32 est 32=3+8+21, on a écrit le nombre 32 sur les trois cartes comportant le 3, le 8 et le 21.

Comment rendre le tour encore plus spectaculaire ?

Afin de renforcer l’impact émotionnel de ce tour vous pouvez:

• Présenter les cartes dans un ordre différent que celui qui consiste à montrer d’abord la carte commençant par le 1, puis la carte commençant par le 2, etc.
• Dire que ces cartes comportent chacune des nombres choisis aléatoirement entre 1 et 100 (on sait que cela est faux, mais ce petit mensonge renforcera l’effet du tour). De toute façon, rare sont les personnes qui connaissent la suite de Fibonacci, et encore plus rares sont les gens qui s’apercevront que les nombres inscrits sur ces cartes suivent un schéma « régulier » (si tant est que la décomposition de Zeckendorf soit quelque chose qu’on puisse qualifier de régulier). Personnellement, je pense que la force de ce tour est ici.
• Faire croire que la couleur de chaque carte joue un rôle (c’est vicieux ça !) dans le fait de trouver le nombre.
• Faire croire que vous êtes le fils spirituel de Madame Soleil (risqué).

J’espère que ce tour vous a plu, moi je retourne auprès de Claudia Schiffer…

Sources:  Fibonacci Magic Cards Brother Alfred Brousseau, Fibonacci Quarterly 10 (Janvier 1972)

Et pour une vidéo (en Anglais) expliquant le même tour, mais cette fois en utilisant la décomposition en base 2 d’un nombre (qui est unique, elle aussi !), vous pouvez regarder ceci.